인공신경망 확장 방법론 구축
-
선행 연구 및 자료 조사
-
현재 확장이 필요한 시스템
- 각 loop 계산에서 필요한 계산시간 확보
-
방법론 구축
parameter 선정
- 상관관계 분석
- Pearson 상관계수, Spearman 상관계수
- feature selection
- 전진선택
- 후진선택
- Recursive Feature Elimination (RFE): 모델을 반복적으로 학습하여 중요도가 낮은 변수를 제거
- PCA (주성분 분석)
-
이건 PINN에 사용을 못하게 되므로 일단 제외하고 생각.
-
1개 loop 결과 재활용해서 다른 PG에서 사용하는 방식 등 고려
1번 루프 (Mori-Tanaka)
리턴 매핑 루프와 결합이 가능하도록 설계
- 분리 시의 장점은?
- 이전에 구축한 시스템과 연계해서 사용가능
- 내부 루프가 변경되어도 사용이 가능하도록?
- Mori-Tanaka는 fiber의 aspect ratio에 따라 나타남. matrix가 탄성, 소성, 점소성인지와는 관련이 없고, 오직 stiffness만이 여기에 관여하게 됨.
- 이건 각 루프가 서로 독립적이어야 한다는 보장이 필요함.
- 그렇다면 첫번째 루프에 내부 루프에 대한 정보가 input으로 포함될 수 있어야할지도?
- 분리하지 않을 경우의 가능한 문제점
-
output으로 필요한 값으로, 유사결정립의 Dstress, stiffness
-
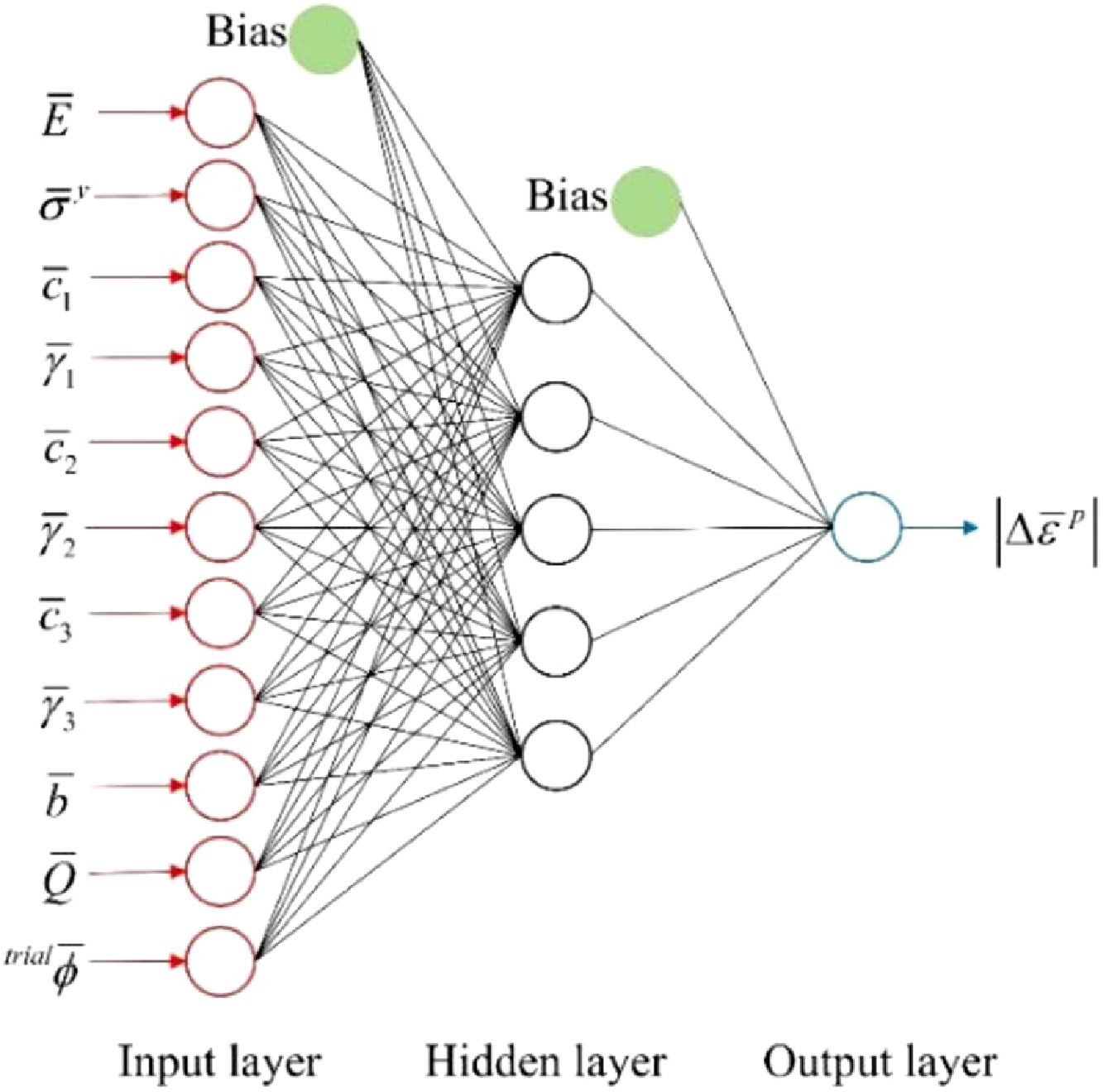
input, output의 크기가 과도하게 커질 수 있고, 학습하고자 하는 시스템이 복잡해질수록 인공신경망 크기가 증가할 수 밖에 없다.
-
결국 matrix와 fiber단위에서 stress를 구한 뒤 voigt 방식으로 결합하는건데, 각 dstrain을 모르니 dstress도 구하기 어려움. 따라서 output값으로 stress를 직접적으로 넣어줘야함.
-
리턴매핑을 분리할 때는 소성 변형의 성질을 활용해서 stress의 component를 줄일 수 있었음.
-
그렇다면 M-T 쪽에서도 비슷한 느낌으로 parameter 수를 줄일 수 있으면 좋을 것 같음.
- 일단 strain은 fiber 혹은 matrix 둘 중 하나만 있으면 나머지는 구할 수 있음
- principal direction으로 변경하는 것 고려
-
- input parameter
- Pseudo-grain dstran
- volume fraction of matrix
- volume fraction of fiber
- stiffness of matrix
- 이건 R-M ann의 output으로서 주어져야함.
- 대체할만한 parameter가 필요함.
- 이전 step의 stiffness
-
- 현 step에서의 변화를 나타낼 수 있는 parameter
- flow stress?
- viscoplastic parameter
- 현 step에서의 변화를 나타낼 수 있는 parameter
- stiffness of fiber
- 과도한 크기 증가의 원인이 될 것.
- μ, λ
-
ν, E
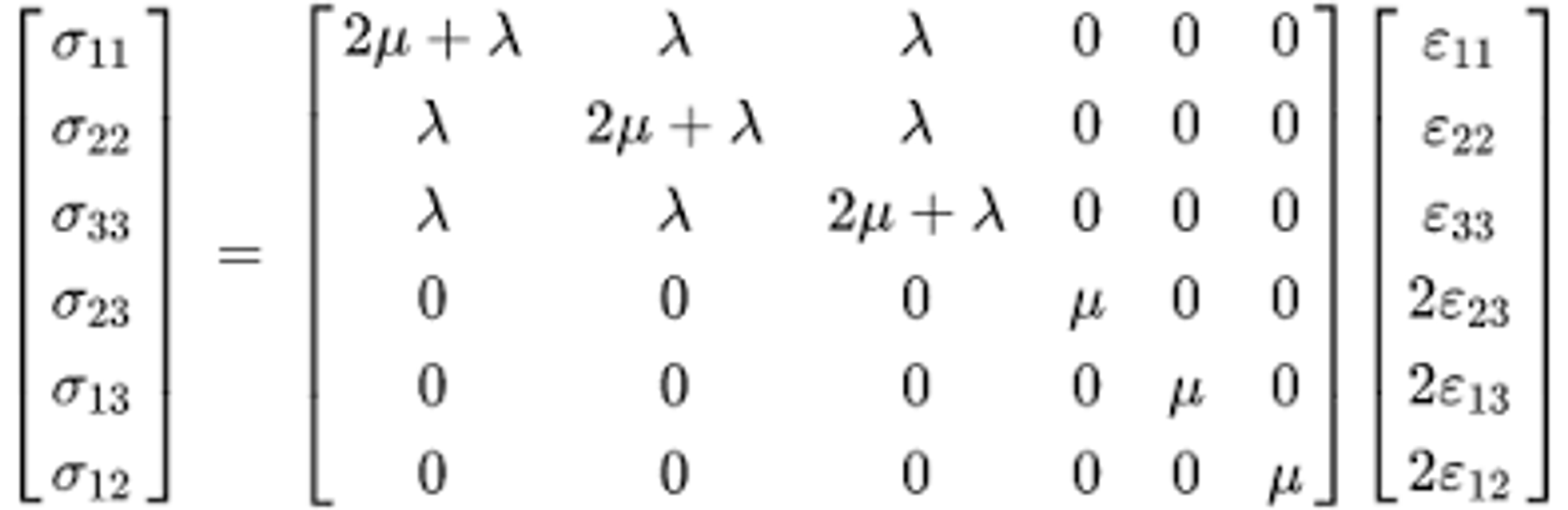
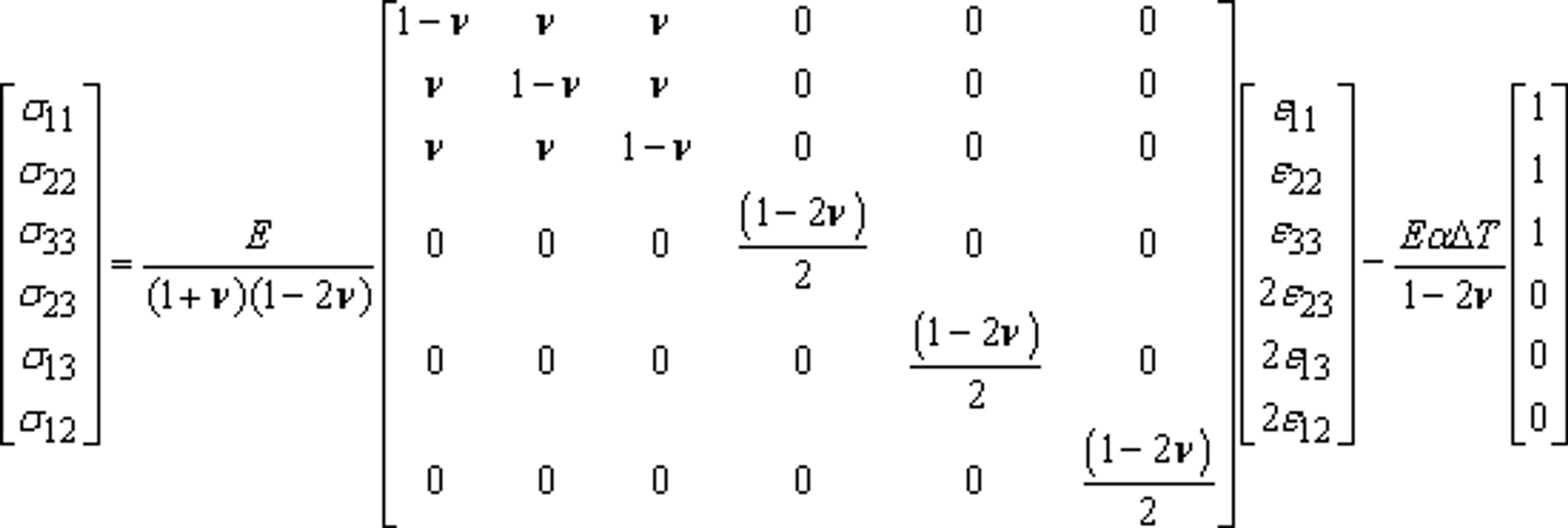
-
- Eshelby tensor
-
이건 계산에 사용되는 값들로 대체가 가능할 수 있음
-
aspect ratio
-
poisson’s ratio
-
분리 방식과 비분리 방식의 장단점이 명확해보임.
리턴 매핑 인공신경망에서 parameter 감축에 대한 아이디어는 통합 ann 구축 시에도 output의 형태로 그대로 가져갈 수 있다. 이건 아닌거 같음. hydrostatic stress의 변화는 결국 dstran0을 알아야 얻을 수 있음.
feed forward neural network calculation 방식임을 강조
선행연구 조사
2023년도 논문에 같은 시스템에서 인공신경망을 적용한 사례가 있었음.
그러나 이 경우 수렴성이 좀 떨어지는 것 같음.?
그리고 딱 SS curve만 보여주지 부품단위의 해석은 어려울 거같음.
Modelling Simul. Mater. Sci. Eng. 31, 075001 (2023).
→ 이걸 보여주고, 더 좋은 활용성을 위해선 모듈화가 필요함을 언급함.
실제로 이전에 구축한 리턴매핑의 경우 더 작은 시스템에 인공신경망을 적용한 결과 더 안정적인 구축이 가능했음.