제안요청서 관련

현재 물성 모델링: 단일 섬유의 동일한 섬유길이 가정 하에서 모델링함.

개선 필요사항

1. 섬유길이의 분포를 고려한 물성 예측

   1. RVE 내 주어진 평균, 편차 조건을 이용한 예측

2. 일반 섬유 외 섬유 사용 물성 예측

   1. 장섬유, flat 섬유 등

3. 두 종류의 섬유가 섞인 사출재 물성 예측

   1. 일반 유리섬유+ flat 유리섬유, 유리섬유+탄소섬유 등

※ Aspect ratio (L/D : 섬유길이/섬유직경, 사출 후 제품 내 값으로 분석)

• 단섬유 사출재 (SFRP) : 15~25 (섬유 함량 : 60 ~ 20%)

• 장섬유 사출재 (LFRP) : 35~50 (섬유 함량 : 40 ~ 20%)
  (제품 내 섬유 길이 : 유리섬유 약 16μm, 탄소섬유 약 8μm)

조사 내용

섬유 길이 분포를 이용한 물성 예측 사례

• Micromechanical modelling of short fibre composites considering fibre length distributions. Composites Part B: Engineering 264, 110868 (2023).

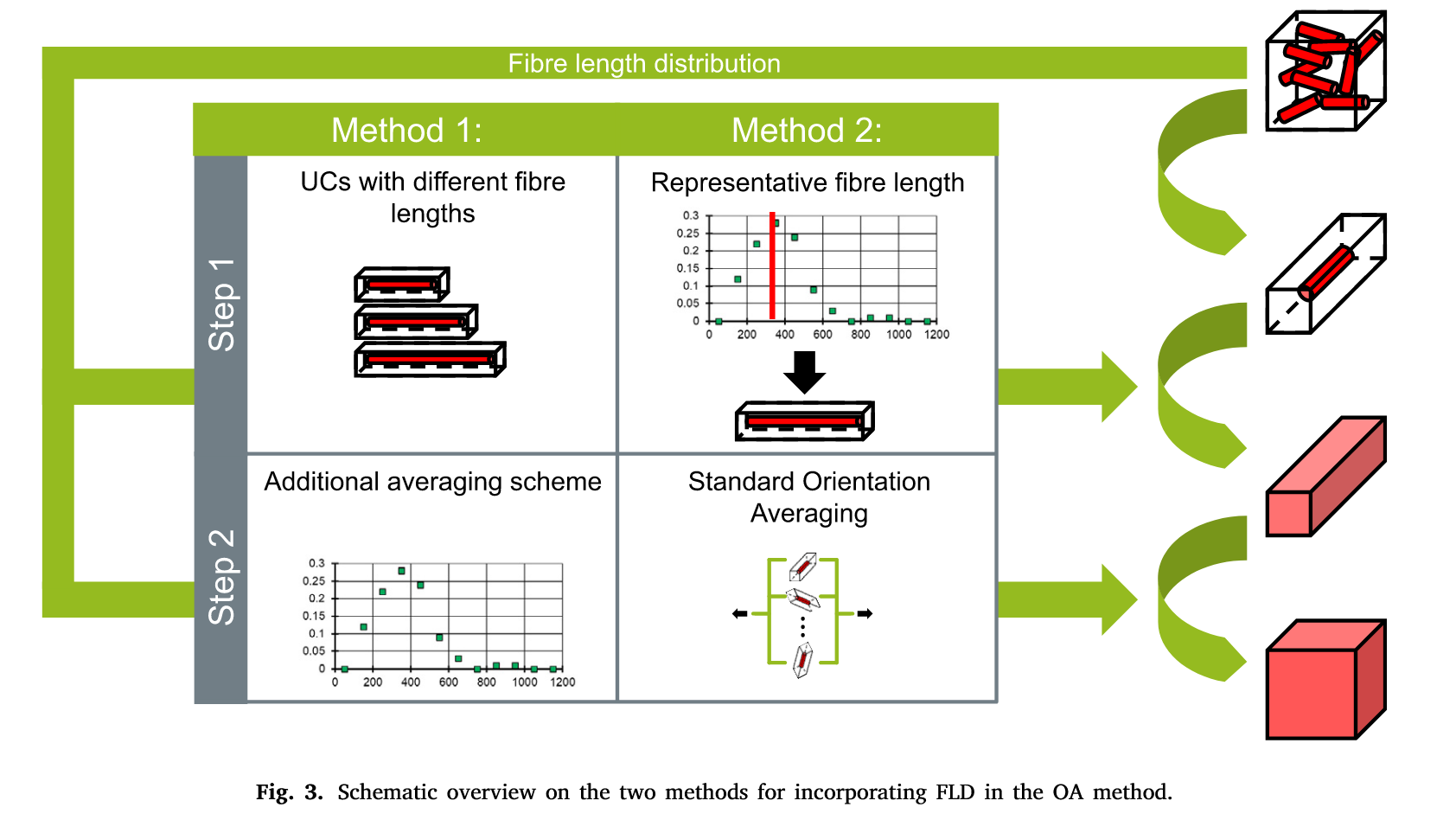
  • general 2 step orientation averaging method에 기반하여 섬유 길이 분포를 고려하도록 확장, 2가지 접근법이 사용됨.

    • 섬유 배향 분포에 대한 평균화 → 섬유 길이에 대한 평균화로 2 step averaging
      • unit cell 단위에서 별도 계산이 들어가서 계산 비용이 증가함.
    • 대표 섬유 길이를 사용하며, 섬유 길이에 따른 stiffness를 고려하여 평균 길이를 계산함.
      • 섬유 길이가 물성에 미치는 비선형 효과를 고려, 단일 섬유 길이를 쓰더라도 더 정확한 반영 가능

  • 여기서도 fiber의 orientation을 반영할 때 2 step homogenization을 쓰긴 했으나, 방식이 우리가 쓴 것과는 약간 다름.
    → 1 step에서 Mori-Tanaka와 같은 mean field homogenization method를 쓰지 않고, 1 fiber를 이용해서 PBC를 적용한 Unit Cell 단위 numerical simulation 결과를 활용함.

  • 두 방법 모두 문헌 상 인장시험 결과와 좋은 일치율을 보이나, 2번째 방법이 계산 성능 상 유리함.

  • 한계점으로 섬유간 상호작용이 단순화 되어있고, 손상 메커니즘이 고려되지 않은 점을 지적함. → 높은 변형률에서는 차이가 발생할 수 있음.

    

• Effects of fiber length and fiber orientation distributions on the tensile strength of short-fiber-reinforced polymers. Composites Science and Technology 56, 1179–1190 (1996).

  • length distribution을 고려해서 modified rule of mixture를 사용한 논문들이 보여서 해당 이론을 제시한 원 논문을 찾아봄

  • 이 ROM은 composite의 UTM의 계산에 사용.

  • fiber의 분포를 표현하는 Weibull 기반 distribution function을 소개하고, 각 distribution에서 대표 length를 구하는 방법이 소개됨.

  • 이 논문은 본래 동일한 length의 orientation이 고려되지 않은 ROM에 length 및 orientation distribution을 고려해서 ROM을 수정한 케이스임. 우리꺼랑 큰 관련은 없을것 같음.

• ★ First pseudo-grain failure model for inelastic composites with misaligned short fibers. Composites Part A: Applied Science and Manufacturing 42, 1892–1902 (2011).

  • 재혁이형이 2 step homogenization 관련해서 참고했던 원 논문

  • 여기선 Pseudo grain을 구축할 때 orientation distribution function(ODF) 뿐 아니라 length distribution function(LDF)도 같이 사용한 것으로 되어 있음.

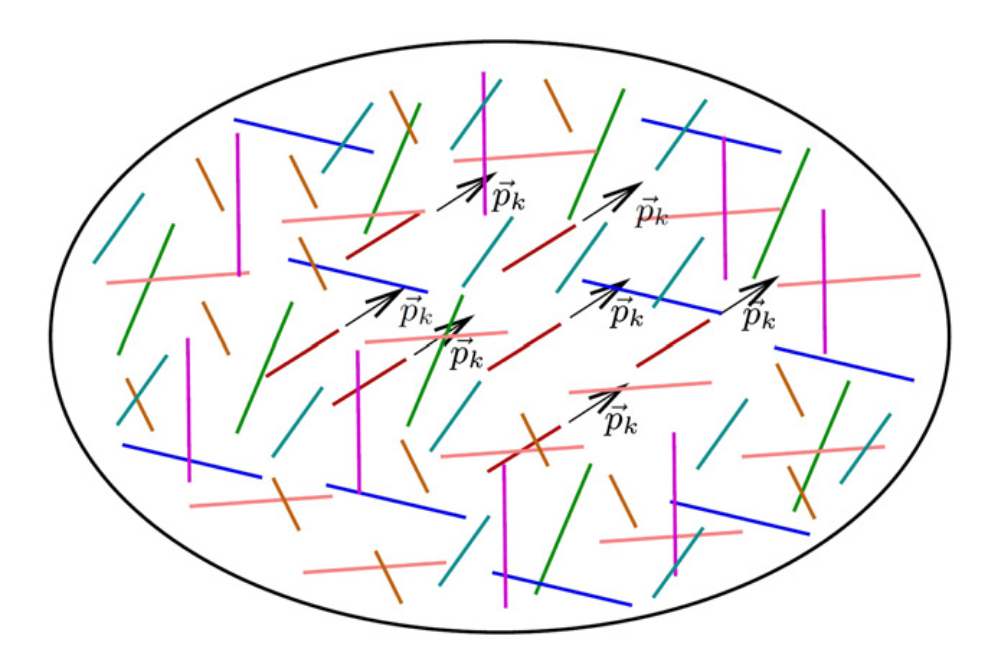
  • 모든 섬유의 길이가 같다고 가정하면, 1개의 ODF만을 사용하여 사용할 수 있으나 여러 length를 가진 경우 discrete length L_i를 갖는 fiber family가 적절한 weight와 함께 고려되어, 각 fiber family가 서로 다른 ODF를 가질 수 있음. (충분한 데이터가 없다면 모든 ODF를 동일하게 가정할 수 있다고 언급)

  • 서로 다른 색으로 표현된 fiber group이 있고, 각기 다른 direction을 가지는 microdomain 형성.

    

  • LDF만 확보된다면 현재 scheme에 바로 적용할 수 있을 것으로 보임. KNN으로 PG를 group화 할 때 orientation 뿐 아니라 length 정보도 활용하여 PG 형성하는 방식.

장섬유, flat 섬유 물성 예측 사례

• The Influence of Fibre Cross Section Shape and Fibre Surface Roughness on Composite Micromechanics. Micro 3, 353–368 (2023).

  • 아직 자세히 안읽어봤는데, non circular fiber를 사용한 경우 interface와 최종 물성 간 영향 분석 사례

  • 같은 cross-sectional area여도 non-circular fiber의 경우 critical fiber length가 줄어든다. → analytical model of critical fiber length에서 볼 수 있음.

    $L_c=\frac{D{\sigma }_f}{2\tau }$

    • σ는 fiber breakage stress, D는 fiber의 diameter

    • critical fiber length는 matrix에 전달된 stress가 완전히 fiber에 전달될 수 있는 최소 길이.

    • flat fiber는 높은 표면적을 가져 stress transfer에 용이함. → 대체로 tensile strength가 크다. (분포를 생각했을 때, 더 많은 양의 fiber가 critical length 이상의 범위에 포함될 것)
      아래 plot은 같은 길이 분포를 가지는 경우 flat(평탄도 K=4)과 circular의 비교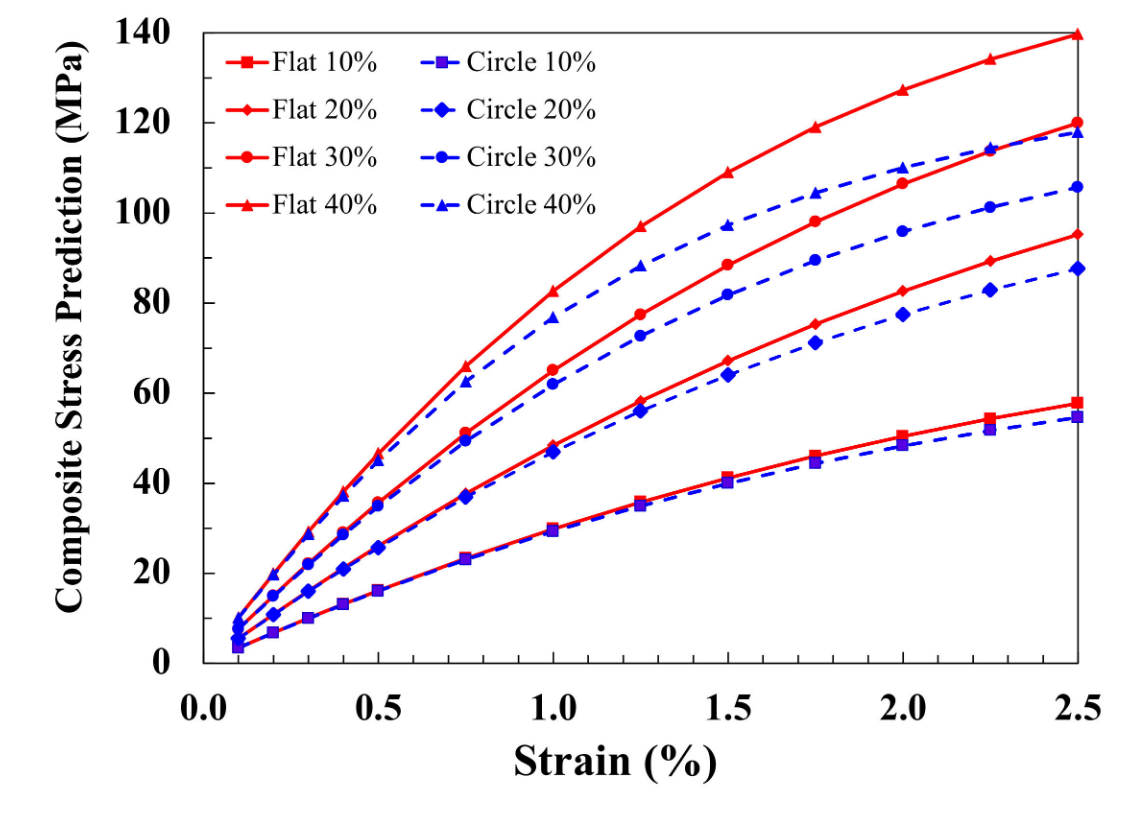

      

• flat 섬유의 경우 사실 eshelby theory 자체에도 우리가 사용한 ellipsoidal inclusion 외에도 flat fiber의 가로 세로 비를 이용한 식을 적용할 수 있긴 함.

• The influence of fibre length and concentration on the properties of glass fibre reinforced polypropylene: 5. Injection moulded long and short fibre PP. Composites Part A: Applied Science and Manufacturing 33, 1641–1652 (2002).

  • SFRP에서 fiber 길이에 따른 기계적 물성 변화 분석 (아래 그림은 단일 길이에 대한 것)

    

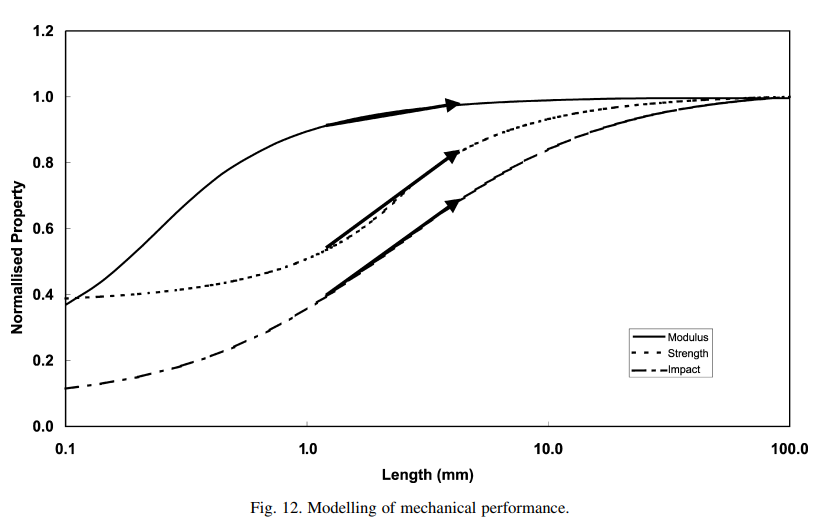
  • 긴 섬유는 성형 과정에서 방향성이 더 무작위가 되어 기계적 특성의 효율성을 일부 상쇄

  • 이로 인해 기계적 특성의 최대치는 특정 섬유 길이 이상에서 포화 상태에 도달

  • 포화 현상 양상이 다른 것은 각 특성마다 필요한 임계 섬유 길이(critical fiber length)가 다르기 때문. 예를 들어, 강성은 비교적 짧은 섬유 길이(약 1.0 mm)에서 최대치의 90%에 도달할 수 있지만, 강도는 7 mm 이상의 섬유가 필요하고, 노치 충격 저항성은 16 mm 이상의 섬유가 필요

이종섬유 물성 예측 사례

• Simulation of Effect of Orientation Distribution Parameters of MWNT Fiber on Elastic Moduli of Hybrid Composites Epoxy/Glass-MWNT (Asian Trans Sci Technol 3 (2013): 1-8.)

  • Stiffness Prediction of Hybrid Kenaf/Glass Fiber Reinforced Polypropylene Composites using Rule of Mixtures (ROM) and Rule of Hybrid Mixtures (RoHM) (Journal of Polymer Materials 30.3 (2013): 321-334.)
  • 두 논문에서 하이브리드 복합재의 탄성 계수를 에측하는 데 해당 이론을 적용하였으며, Ec=Ec1Vc1+Ec2Vc2로 각각의 체적 분율을 기반으로 기계적 특성을 예측
  • 이 때의 가정은

  1.두개로 분리한 복합재 시스템 사이에 interaction이 없음을 가정.

  2.동일한 변형 조건을 적용하여, 각 시스템의 변형이 동일하다고 가정.

  3.힘의 평형 조건을 만족해야 함.

  • Rule of hybrid mixture를 사용. 두 종류의 섬유가 사용된 복합재에 대해 각각 분리하여 rule of mixture 적용.

    

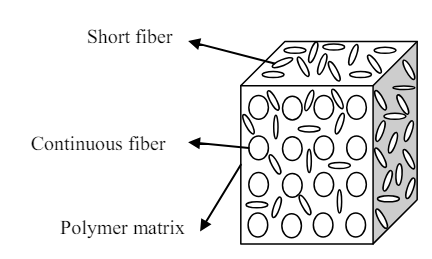
  • 섬유-섬유, 섬유-matrix 간 interaction 등을 고려하였을 때, 복합재의 물성이 증가하거나 감소하는 hybrid effect가 나타나기 때문에 rule of hybrid mixture를 적용한 결과와 실제 오차가 나타날 수 있음.

  

  

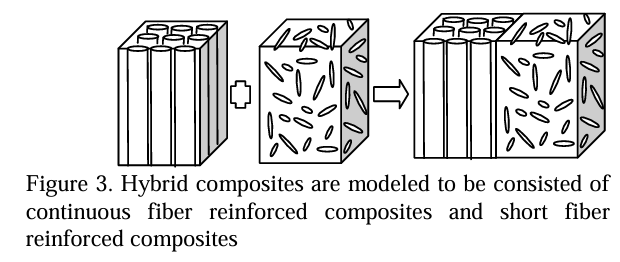
  해당 figure는 첫번째 논문의

• On the elastic modulus of hybrid particle/short-fiber/polymer composites (https://doi.org/10.1016/S1359-8368(02)00013-6)

---

---

• 찾아본 논문들 (내용 정리x, 곧 할 예정) (뭔가 애매해서 다른 논문들 조사 중)

1-1) Elastic properties of injection molded short glass fiber reinforced thermoplastic composites

(https://doi.org/10.1016/j.compstruct.2020.112850)

1-2) Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements

(https://doi.org/10.3390/fib9050032****)

• Experimental analysis and theoretical modeling of the mechanical behavior of short glass fiber and short carbon fiber reinforced polycarbonate hybrid composites (Polymer Composites 37.4 (2016): 1238-1248.)

  • Short fiber - E-glass, carbon, milled carbon 세 종류의 fiber를 이용하여 1종류 단섬유 SFRP, glass-carbon hybrid SFRP, glass-milled carbon hybrid SFRP를 사출성형으로 제작.
  • 각 short fiber의 초기 길이는 각각 3 mm, 6 mm, 0.22 mm, 사출 성형 결과 섬유 breakage에 의한 평균 길이는 각각 0.204 mm, 0.162 mm (E-glass, carbon fiber) - fiber length distribution을 광학 현미경을 이용하여 측정.
  • fiber, matrix의 기여도(X, Y, Z), Critical fiber length, L_c, and Fiber orientation factor 계산을 통해 composite이 받는 stress를 다음과 같이 표현 (Kelly-Tyson model)

  ${\sigma }_c={\eta }_0(X+Y)+Z$

  • 수식 정리하다가 꼬여서 다시 정리해볼게.

  • 논문의 요지는 hybrid fiber composite의 물성 예측을 섬유-matrix 간 interaction을 고려하여 interfacial shear stress term이 들어가는 Kelly-Tyson model을 이용하여 stress-strain 관계를 정의했고, 해당 식이 SFRP, hybrid SFRP에 대해 tensile test를 진행한 결과, tensile strength를 잘 예측함을 보임.

    

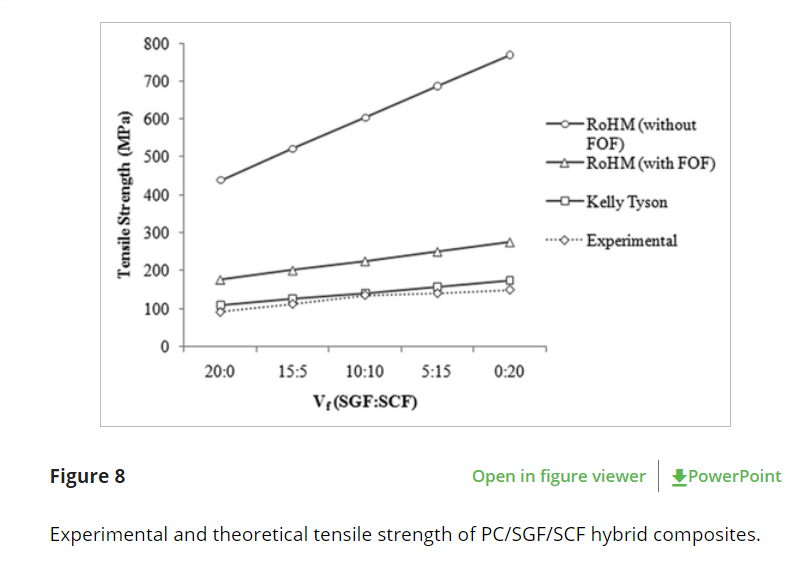
• A model for fiber length attrition in injection-molded long-fiber composites (Composites Part A: Applied Science and Manufacturing 51 (2013): 11-21.)

  • long fiber 10-13 mm length를 사출 성형 시 발생하는 섬유파괴에 의한 length distribution을 계산 ( 결론적으로 길이가 긴 섬유의 사출 성형 시 원래 길이를 유지하는 섬유는 거의 없으며 1-2 mm 길이를 갖는 섬유가 주로 분포함을 예측 및 실험적으로 확인)
  • 섬유 길이 l_i = i*delta_l로 잡았고, 논문에서 따로 언급은 없으나 delta_l 을 가장 짧은 섬유보다 작게 설정하여 섬유 길이가 보존되도록 계산
  • 섬유 전체 길이(L_t)가 보존된다는 가정하에 섬유가 파손 됨에 따라 섬유 길이 l_i를 갖는 섬유 수 N_i가 어떻게 변하지는지를 식으로 표현

  $L_t=\sum N_i{l}_i$

  $d{L}_t/dt=0$

  $d{N}_i/dt=-P_i{N}_i+{\sum }_k{R}_{ik}{N}_k$

  • 섬유 파손 확률 P_i와 섬유 파괴에 의한 부모섬유에서 자식섬유 생성 확률 R_ik를 계산하여 fiber length distribution을 계산한 것과, 실험 ( polymer matrix를 태워 섬유 확보 및 길이 측정) 값을 비교

  

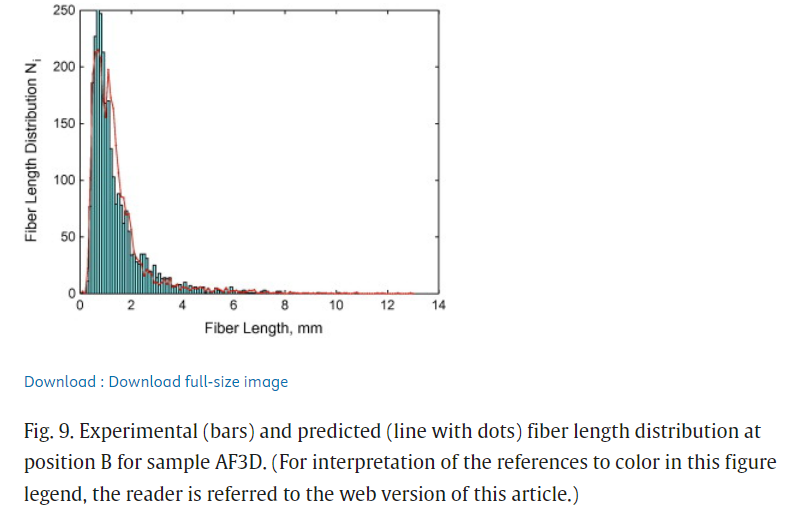
고려가 필요한 부분들

• 이종 사출 시 fiber orientation distribution은 moldex로 구현이 안될거 같은데 이 부분 어떻게 해결해야 할지?

  • 현재 구축된 scheme의 경우, Moldex에서 제공되는 섬유 배향 텐서 a_ij 로 부터 maximum entropy model을 사용해서 섬유배향 분포함수 ψ(p)를 재구축함.

  • 지난번 과제에서 재혁이형이 관련해서 matlab 코드를 작성해서 재구축을 구현했음.

  • 그러나 이 과정은 반복 과정이 필요한 numerical 방법이어서 효율성을 위해 인공신경망을 구축했음.

  • 이 부분이 이종 사출에서도 적용이 가능할지는 의문임.

    • 일단 moldex나 moldflow에서 섬유 배향 텐서는 받아야 하는데 이종사출에서 이게 되는지
    • 마찬가지로 maximum entropy model의 적용이 가능할지
    • 2변수 bingham distribution으로 표현이 가능할지