문법
- if문
- if (logical expression) then
statements
elseif (logical expression) then
statements
else
statements
endif
- if (logical expression) then
- Write
- Format 없는 경우
- print *, var1, var2,…
- Format 있는 경우
- write(u,f) list
-
u는 출력장치 번호, f는 format 번호, list는 출력할 변수(,로 구분됨)
-
!write(*,10) i,j,dsum ← 출력 변수가 i,j,dsum으로 3개
!10 format(2i5,5x,f5.2) ← format number =10일 때의 format을 지정해준 것!여기서 괄호 속 f는 format 형식으로,e f는 실수인데 각각 지수 표시(E+2등)/ 고정형식(숫자 그대로) , a는 string, d는 double precision,i는 integer, x는 space, /는 줄넘김
!Fw.d면 실수인데 숫자를 적을 전체 칸을 w으로 하고, 소수점 아래 d만큼 표시
!0.026을 E8.1 이면 0.3E-1
!format 안 파라미터는 write할 출력변수(여기선 3개)에 대해 각각 형식을 지정해준 것
-
- write(u,f) list
- Format 없는 경우
- DO문 (loop)
-
Do문은 loop를 하는 것
do label var=a,b,c
statements
label continue
이 때 a, b, c는 각각 var의 초기값, 종료 한계, 증가 step을 의미 -
예시 - 1-n까지 합
- integer i, n, sum ← i,n,sum variable에 대해 integer라는 자료형 부여/ loop 내부 변수 i에 대해서도 부여해줌
sum = 0
do 10 i = 1, n ← loop label은 10, 초기값1, 종료값n
sum = sum + i
write(,) ‘i =’, i
write(* ,*) ‘sum =’, sum
10 continue
- integer i, n, sum ← i,n,sum variable에 대해 integer라는 자료형 부여/ loop 내부 변수 i에 대해서도 부여해줌
-
변수
-
Z는 z방향 coord vector, (Z1, Z2) ⇐ element 2개의 경우
-
P는 Total displacement vector, (u1, u2, w1, w2)
-
AL은 length of element
-
EA는 young’s modulus * area
-
E는 young’s modulus
-
ARA는 area
-
B: beta
-
NV : number of variables
-
QFI는 external loading, (ue1, ue2, we1, we2)
-
IBC는 boundary condition information, boundary condition 있으면0, 없으면1 이때 해당 자유도에 외력이 가해지면 0이어야 한다.(prescribed)
-
NDSP는 number of earthed springs,
-
ID14S 는 id of earthed spring,
-
AK14S는 stiffness of earthed springs, 번호 작은것 부터 순서대로 (ID14S와 매치됨)
-
AK15는 additional spring 있어서 NV=5일때만 유효
-
ANIT: initial load, N0
Subroutine
-
element: internal force vector(qi, FI) 계산 및 element tangent stiffness matrix(K, AKT) 계산
- IMOD 1,2,3 일 때 전자/후자/둘 다 계산
- IWRIT? → 0이 아니면 writes out FI and AKT on channel IWR
-
INPUT : geometry, property, BC, load 등의 정보를 input
-
‘IRE’에서 data 입력받음

-
-
ELSTRUCT : Element striffness matrix (AKTE(4,4))를 받아 structured stiffness matrix(AKTS(NV,NV))로 변환
→ earthed springs 추가, NV=5일 때(additional spring이 있음, Ks5) variable 1-5 사이 linear spring 추가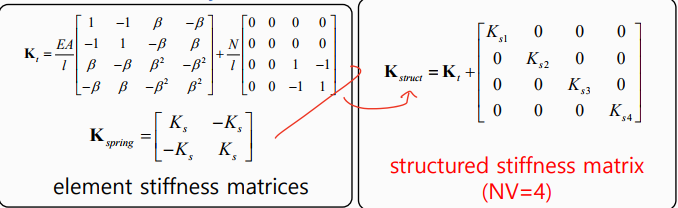
- Qi 가 있는 IMOD 1,3에 대해서
- earthed spring이 있는 dof (4번) 에 대해 해당 DOF의 Qi update
-
Qi + K_earthedspr * P
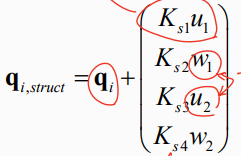
-
- additional spring(Ks5)이 있는 경우 → Qi1 수정, Qi5 추가
- earthed spring이 있는 dof (4번) 에 대해 해당 DOF의 Qi update
- K가 있는 iMOD 2 3에 대해서
-
AKTS(structured Stiffness matrix) =0행렬로 만든 뒤 AKTE값 대입 후 additional spring 값 대입
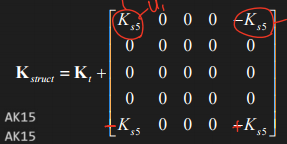
-
earthed spring이 있는 경우 structured K 의 해당 자리에 더해줌
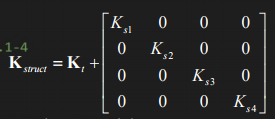
-
- Qi 가 있는 IMOD 1,3에 대해서
-
BCON : constrained displacement 를 external force로 변환 (load control화)
- AK에 boundary condition 적용

- IBC는 boundary condition information, boundary condition 있으면(prescribed) 1, 없으면(free) 0? 반대 이때 해당 자유도에 외력이 가해지면 0이어야 한다.
- case1: prescribed displacement P_p=0 (IBC(i)=1)일 때
-
행렬식 2행의 경우 dummy equation
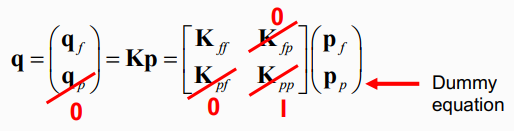
-
- case2: constrained displacement Pp ≠0
-
nonltb
순서 및 변수 지정
nonltb → input → iter → force
DOUBLE PRECISION QFI(5),PT(5),AKTS(25),D(5),GM(5),FI(5),REAC(5), BETOK,X(2),Z(2),E,ARA,AL,AK14S(4),ANIT,AK15, ARN,POISS,ALN,AN
INTEGER IBC(5),IRE,IWR,I,NV,ID14S(4),NDSP,ITYELDOUBLE PRECISION E,ARA,AL,QFI(NV),X(2),Z(2),ANIT,AK14S(4),AK15, ADUM1
INTEGER NV,IDUM,I,NDSP,ID14S(4),IBC(NV)DOUBLE PRECISION PT(NV),QEX(NV),REAC(NV),FI(NV),GM(NV),AKTS(NV,NV),D(NV),AKTE(4,4),X(2),Z(2),E,ARA,AL, AK14S(4),AK15,ARN,POISS,ALN,SMALL,FNORM,GNORM, RNORM,BETOK,BAS,BET,AN,ANIT
INTEGER IBC(NV),ID14S(4),NDSP,ITYEL,NITMAX,IMOD
COMMON /DAT/ X,Z,E,ARA,AL,ID14S,AK14S,NDSP,ANIT,AK15
COMMON /DAT2/ ARN,POISS,ALN,ITYELDOUBLE PRECISION Z(2),P(4),X(2),AN,ANIT,E,ARA,AL,ADUM1,ADUM2,ADUM3
INTEGER IWRIT,IWRFORCE(AN,ANIT,E,ARA,AL,X,Z,P,IWRIT,IWR,ITUM, ADUM1,ADUM2,ADUM3)
챕터3
This is the problem previously discussed in Section 3.2 and defined in (3.39) and Figure 3.3. The responses are as shown in Figure 3.4.
The following data relates to a solution using Green’s strain for the compressive
regime. It is obtained using displacement control so that no structural equations are
solved.
4 1 500000. 100. 0. 0. ; NV,ITYE(Green),E,ARA,POIS,ANIT,
0. 2500. ; x-coords.
0. 0.00 : z-coords.
0. - 1000. 0. 0. ; fixed displ. vector 1 - 1 1 1 ; Bdry condn. code.
0 ; no earthed springs
6 0 ; load inc. factor, no. of incs., write control
0.2
0.001 1 ; convergence tol., iteration. type (N—RELEMENT
-
GENERAL TRUSS 에 대해 internal force vector(qi, FI) 계산 및 element tangent stiffness matrix(K, AKT) 계산
-
변수
-
N: INPUT TOTAL FORCE IN BAR
-
P: TOTAL DISPLACEMENT VECTOR
-
Z,X: INPUT, Z, X COORDINATE VECTOR
-
ALO: INPUT, ORIGINAL LENGTH OF ELEMENT
-
ALN: NEW LENGTH
-
ARN: INPUT, CURRENT AREA
-
ITY: STRAIN MEASURE
-
ALAM: ALO/ALN, LENGTH RATIO
-
X21D: X(2)-X(1) + P(2) -P(1),
-
Z21D: Z(2)-Z(1) + P(4) -P(3)
-
CON: AN/ALO, N/ORIGINAL LENGTH , N=SIGMA*A
-
-
코드 진행
-
우리껀 ITY = 1
-
QI 계산
-
CON=FORCE/ORIGINAL LENGTH 계산
-
CON=ALO
-
-
