MLDL 중간고사

<Overfitting & Regularization>

• 학습에 따라 training loss는 계속 줄어들지만 validation loss는 overfit에 의해 어느 순간 증가
  (데이터의 noise까지 학습, 모델이 복잡할수록 overfit쉽게 발생)

Early stopping

• 일정 주기로 val set으로 테스트해보고 오버핏 발생 시 정지 가능
• 그렇다면 실제 관심있는 accuracy 등을 metric으로 쓸건지, 아님 log loss 처럼 loss를 쓸건지?
  → validation loss에서 overfit 안생겨도 actural metric에선 나타나는 경우 있고, metric마다 overfit 나타나는 시점이 다르므로,
  관심있는 metric을 쓰는게 좋음

Regularization

• 어떻게 predictor들을 선정할 것인가? 모든 가능한 케이스를 다 해보는건 비효율적
  → Shrinkage method 사용 가능

  Ridge Regression

  • Least square 식에서 parameter 크기에 대한 term을 추가함, 서로 trade off

    

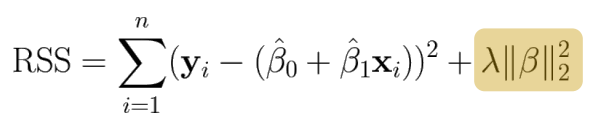
  • λ 크기는 CV 사용하면 됨. 커질 수록 각 beta가 0에 수렴

  • 각 perdictor 간 scale이 다르므로, 이를 맞추는 scaling이 필요하다.

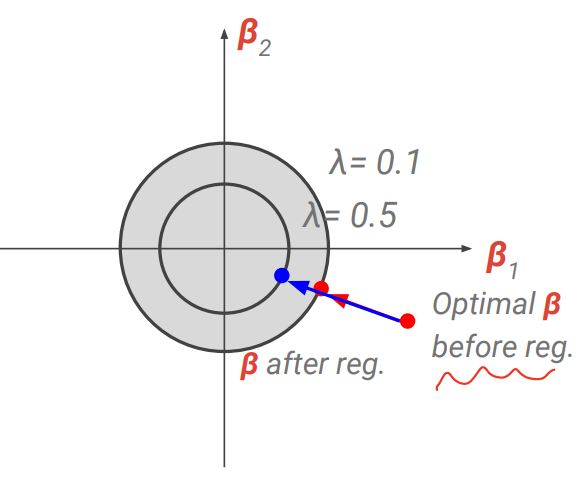
  • λ 가 커짐에 따라 regularization 이 더 커지고, overfit 줄며, variance 작아지고 bias(모델 rigidity에 의해 패턴을 반영하지 못하는 정도)가 증가.
    → 둘 간의 trade off로 MSE가 가장 최소인 model을 선택할 수 있게 됨.

  • regularization 후에도 모든 predictor는 남게됨.

    

    

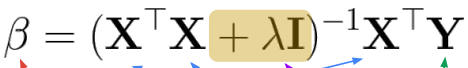
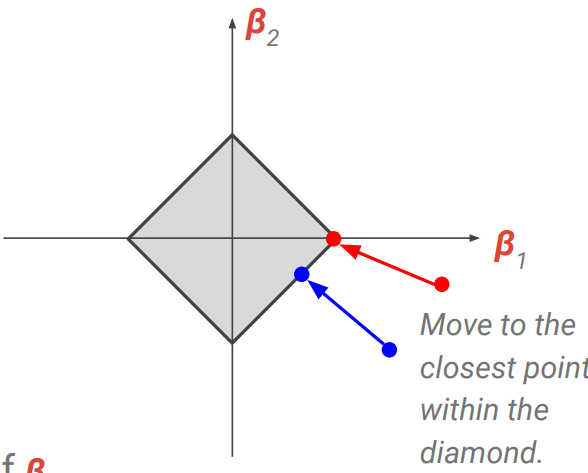
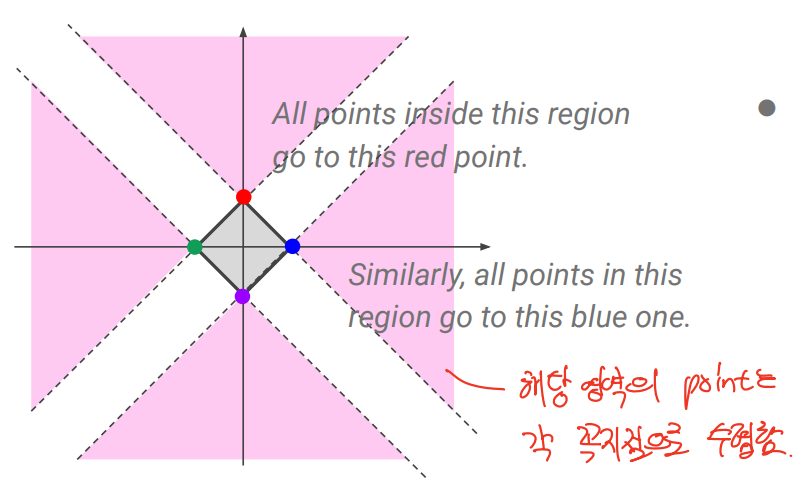
  Lasso regression

  

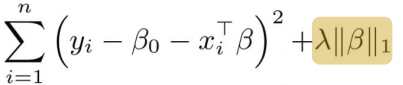
  • variable selection으로 이어지는 특성이 있음. 마찬가지로 lambda 는 CV로 고름
  • 차원이 커질 수록 더 쉽게 sparse model 로 이어지게 됨

  

둘 간의 차이

• lambda가 매우 클 경우 lasso는 bias 빼고 다 계수가 0이 되지만 Ridge는 연속적으로 다 줄어듬

• 실제 function이 적은 predictor 에 대한 함수일 경우 lasso가 낫다. 그러나 실제 함수를 모르므로, CV 등을 통해 어떤게 더 나은지 판단 가능

• regression 과 classification 둘 모두에 사용 가능

• 데이터 해석 측면에서 좋으나, 예측 정확도는 비교적 떨어짐

• predictor space를 나눠서 분류 후 class내 데이터 평균값이 대표값이 됨.

Regression Tree

Step2: 예측값 선택

• least square(예측-정답 제곱) 최소화하는 prediction 대표값 정해야함

• 이를 위해 MLE사용 (f’(c)=0) → 각 region training example의 평균값이 사용됨

  

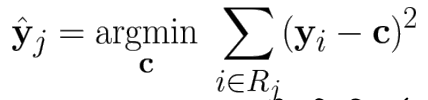
Step1: Region 분리

• RSS 최소화가 ideal이나, predictor도 많고 나눌 수 있는 경우의 수가 많아 불가능

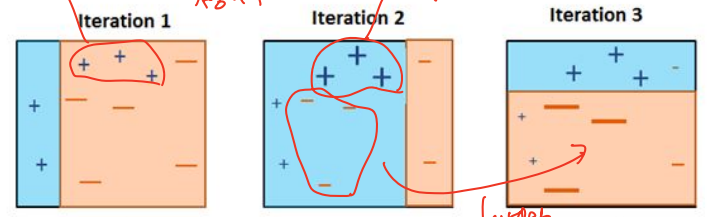
• Recursive binary splitting 방식으로, top down 방식과 greedy 방식 2가지가 있음

• 모든 region에서, 모든 predictor에 대해 모든 가능한 cut point를 정하고, 이 중에서 가장 RSS가 낮아지는 cut point 선택
  → 이 중에서 분리 시 RSS가 최소화되는 region, predictor와 cut point를 정해 분리
  → 이걸 stop criterion 만족할 때까지 반복함.

Tree Pruning

• Decision tree도 overfit이 가능함 → 방지 위해 pruning 진행

• overfit 줄이기 위해 model complexity를 줄이지는 못하고, parameter가 없으므로 regularization도 불가
  → node를 줄여서 덜 쪼개는 방식이 overfit 줄일 수 있다.

• Pruning parameter α를 사용해서 RSS에 tree 크기 term 추가

  

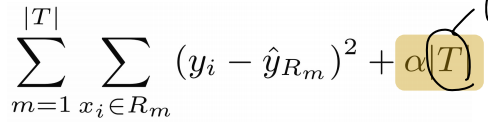
• 우선 recursive binary splitting을 끝까지 진행한 후 weakest link pruning을 진행함.
  → alpha 구하기 위해 k fold CV를 진행하고, 다시 pruning을 진행하여 alpha 선정. 최종 pruning 구조 선정

  Weakest link pruning

  • 각 region을 모든 경우의 수에 대해 합쳐보고, 가장 손해가 적은 merging 을 선택함.

  • CV로, 어느 정도까지 해야 하는지 결정해서, 결정된 size까지 pruning 진행

Classification Tree

• prediction 이 categorical reponse
  → 쪼갤 때 MSE를 구할 수 없고, 평균내기도 불가능하므로, counting 방식으로 다수결로 가장 많은 categorical response가 대표값이 됨

• 그 외 과정은 같으나 세부적인 식만 차이가 있음

Step2: 예측값 선택

• majority vote를 사용

  

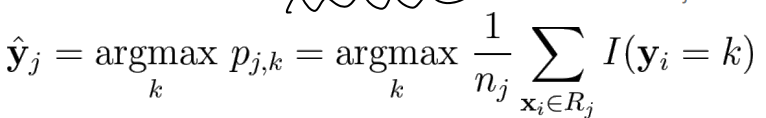
Step1: region 분리

• 마찬가지로 recursive binary splitting 을 사용하지만, 여기선 고르는 기준이 lowest classification error rate이 됨.
  → 여기에서 사용하는 것이 impurity 개념인 enthropy와 Gini index (impurity가 낮음=pure하게 같은 category 인 것 끼리 있음)

• Enthropy → category 5개이고, region 내 data가 모든 category에 균등하게 분배된다면 각 category k의 p가 0.2이고, impurity=-5*0.2log0.2

  

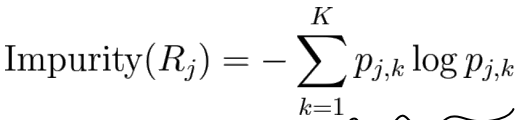
• Gini index → 같은 케이스에서 50.20.8

  

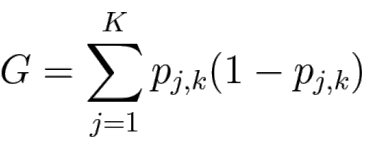
pros and cons of decision tree

• 실제 decision boundary가 linear한 경우 linear model이 유리하고, axis aligned boundary면 tree가 유리

• graphically 보여주기가 좋음.

• dummy variable없이도 categorical predictor도 handle가능

• accuracy가 떨어지는 편이며, robust하지 못해 data의 작은 변화만으로 최종 tree가 크게 달라짐.

Bootstraping

• 머신러닝에서 data 수가 적은 경우 사용 가능
  → 단일 데이터셋을 리샘플링해서 많은 샘플을 생성하고, 주어진 predictor나 머신러닝 방법과 관련된 불확실성을 정량화하는데 사용
  → 복원 추출을 이용해서 dataset을 original로 유지함

• original data가 3개 set이 있으면, 이 중에서 복원추출로 3개를 뽑아 bootstraping하고, 이걸 B번 반복하여 각 parameter 추출 → noise가 독립적이므로 평균을 내면 error를 줄일 수 있다.

• 그러나 I.I.D 조건이 필요하다.

  Bootstrapping vs CV

  • CV처럼 k개 bootstrap 만들어서 k-1개로 학습한 뒤 k번째 남겨둔걸로 validation 방식
    → bootstrapping에선 사용 불가, K-fold의 경우 각 k fold에서 overlap이 없기 때문에 사용 가능하지만 bootstrap에서는 overlap이 발생. 이는 복원추출이기 떄문이며 원래 데이터셋의 2/3 정도 만이 각 bootstrap sample에 나타나게 됨.

Bagging(bootstrap aggregation)

• B개의 bootstrap을 만들고 prediction을 평균/다수결 냄

  

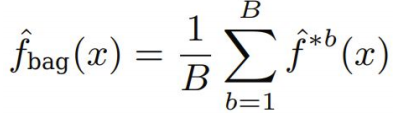
• 결과 자체는 같은 문제에 대한 답이므로 모델에 무관하게 사용 가능해 모든 분류/회귀 모델에 적용 가능

• bias에 대한 cost 없이 variance를 줄일 수 있다.
  ← 각 분산이 σ^2인 n개의 observation에서 평균 observation의 variance는 σ^2/n임.
  같은 모델이므로 complexity동일하고, bias는 같음. 그러나 하나가 틀려도 다수결 방식이므로 variance가 낮아진다.

• 대신 n번의 model training이 필요하므로 계산 비용 측면에서 실용적이지 않을 때가 있다.

• combined model의 expected error는 각 b개의 single model 평균보다 항상 더 좋거나 같다.
  → Jensen’s inequality로 증명

• combined model의 expected error는 각 b개의 single model 평균의 최대 1/B만큼 작아질 수 있다 → 각 B개의 model이 완전히 독립일 경우 covariance가 0이 되면서 1/B로 최대한 작아지며 반대의 extreme case에선 둘이 같게 됨.

Bagging with Decision Trees (Random forest)

• bagging과 마찬가지로 bootstrapped sample에 대해 여러개의 decision tree를 구축.

• 이 때 tree 훈련 시 매 split마다 p개 predictor 중 m개만을 선정해서 m개 predictor subset으로만 split 반복 → 다수결로 선택. 트리마다 다른게 아니라, 자를 때 마다 sampling

• 마찬가지로 variance를 줄일 수 있다.

Boosting

• bagging은 여러 bootstrap을 생성해서 각각 모델 훈련 후 합치는 방식이면, boosting은 sequential growing 방식으로, 앞의 정보 활용해서 뒤 step의 방향성을 유도하는 방식 (weak learner)
  → 앞의 학습에서 못 fitting한 example에 대해서 학습을 진행

• base learner를 순차적으로 결합하되, 이전에 학습된 base learner의 performance를 이용함.
  → 이전모델에 기반해 각 training example의 weight를 조절함
  → 맞게 분류되면 down-weight, 틀리게 분류된 경우 boost

• 여러 base learniner에 대해 학습 반복해서 전반적 performance를 측정

• 모든 base learner는 performance에 기반해서 weight를 곱해 선형결합됨.

Adaboost

• boosting for classification

아래는 2개 class에서의 example

각 step t에서, ht: base learner, Dt: sampling weight distribution, εt= Dt 하에서의 error rate , αt=log (success rate / error rate)으로, error rate 1에 가까울수록 -∞, 0에 가까울수록 ∞

1. uniform distribution D1=1/n으로 initialize
2. 각 t step에서,
   1. Dt 이용해서 training set sampling한 뒤 base learner ht 학습
   2. error rate 계산 후 αt도 계산
   3. 모든 n개의 dataset에 대해서 구한 αt 이용해 새로운 data distribution(D_t+1) update
      → 맞는 example이면 weight 작아지고, 틀리면 커짐
      → 구한 D를 normalizing해서 sum이 1이 되게 함
3. final classifier는 base learner를 αt 이용해서 weighted sum으로 구함

• boosting이 작동하려면 base classifier의 success rate가 최소한 50퍼 이상이어야 함.
• 알고리즘 상 stagewise selection과 유사함
  • stagewise additive learning with exponential loss과 같음

Boosting for regression

• 각 step에서 current model로부터 새 base model을 residual(정답-예측)로부터 피팅
  → residual 큰 example에 더 포커스 맞춰 학습

• Adaboost에서 Dt처럼 각 step에서 residual 을 확인

• bagging, random forest, boosting등은 decision tree의 낮은 accuracy를 보완할 수 있는 좋은 방법

Support Vector Machines

• 선형 회귀, DA에서처럼 p(y|x)를 추정하지 않고, 아예 확률을 사용하지 않는 방식.

• p차원 space를 p-1차원 flat hyperplane으로 분리하며, plane의 equation은 normal vector로 구성
  → hyperplane 기준 0 이상/이하로 지역구분

• 2개 class간 margin을 최대화 하는 방식으로 분리. margin은 hyperplane과 2 class 사이 가장 가까운 거리

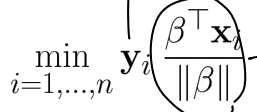
Support Vector Machines for Linearly Separable Cases

• binary classfication을 상정할 것

• Margin-based classifier → normal vector β와 point vector x를 내적했을 때 0 이하/이상으로 class 구분

• Margin에 Maximum likelihood estimator 적용해서 풀 경우 optimazation problem (primal problem)의 direct solution 구하기 어려움 → primal problem을 dual problem으로 바꿈

Primal problem

• β 와 x의 내적의 부호로 분리를 하는데, 이 때 x대신 양의 상수 α를 곱한 αx를 사용해도 부호는 불변 → y β x ≥ 1 이 되도록 beta를 rescale → 최소값이 1이 됨.
  → optimization problem은 argmax(1/||β||)=argmin(||β||)=argmin(||β||^2/2) S.T. y β x ≥ 1 이 됨.

• 이건 origin에서 부터 가장 크기가 작은 beta를 고르는 primal problem이 된다.
  → 이 때

• equality constraint g(x) 조건이 딸린 f(x)의 optimum은 Lagrange multiplier λ를 이용한 Lagrangian의 stationary point를 찾아 구할 수 있다.→ x와 λ를 partial derivative가 0가 되도록 해서 찾음

  

  

  

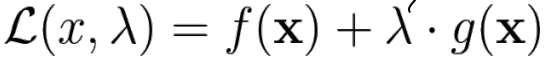
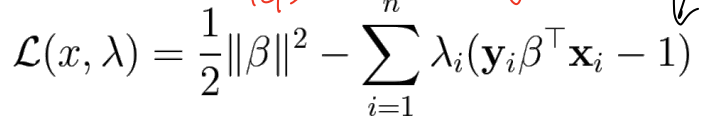
• 2개 식이 나오는 dual problem이 된다.

  

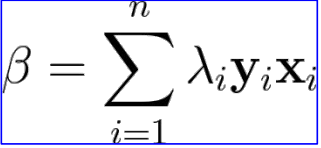
• 1번 식 풀어서 beta 구하고, 이를 다시 대입

  

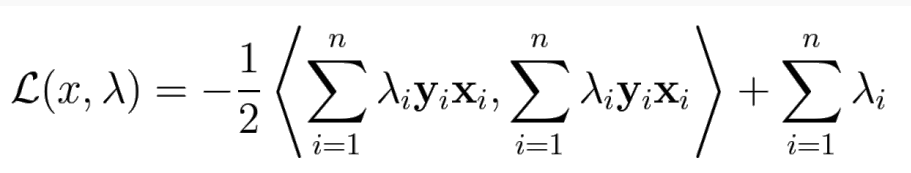
• 마찬가지로 2번째 식도 풀면 final 식은

  

  

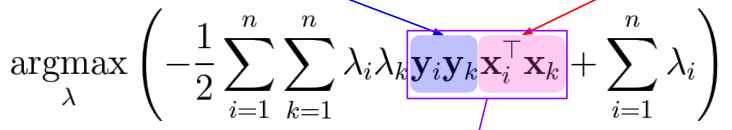
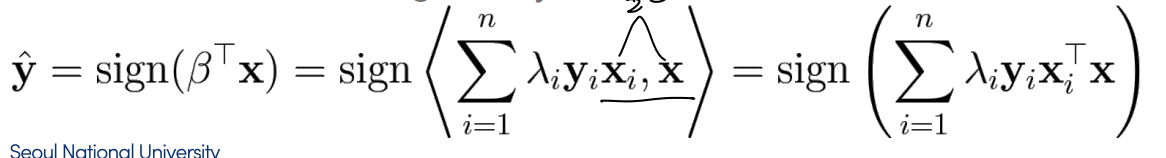
• 이 떄 두 실제 label이 같으면 파란 부분이 +, datapoint가 같은 편에 있으면 + 이고, 반대로 label 다른데 다른 편이면 둘 다 -로 곱하면 양의 값이 됨. → maximize 위해 λ은 0이 되고, 그렇지 않고 음의 값 가지면 λ가 양의 값을 가져야 함.

• λ는 즉 example이 분류되기 어려운 정도를 나타냄

• 이 때 λ는 대부분 0이지만 margin 위의 example은 non zero λ를 갖고, 이를 support vector라 한다.

• 식을 보면, positive class의 support vector와 negative class의 support vector가 서로 compete하며, support vector 제외한 나머지는 0이 되어 참여하지 않음

  

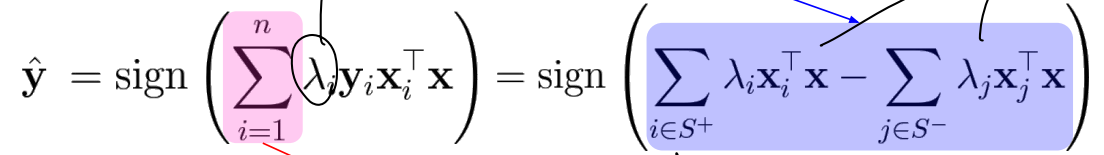
Support Vector Machines for Linearly Non-separable Cases

• noise가 있는 경우 boundary가 크게 바뀌는 문제가 있고, 서로 seperate하지 않은 경우 선 1개로 완전히 구분 어렵다.

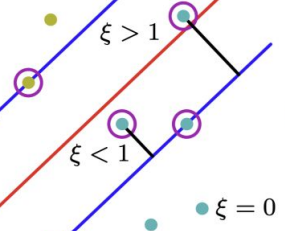
• 이를 위해 slack variable인 ξ i를 각 x i에 도입하여, margin을 늘리는 동시에, misclassification rate를 줄이고자 함 → ξi는 constraint yi βT xi ≥ 1이 위배된 정도를 나타냄. 0이면 위배되지 않은 것이고, 0-1 사이면 decision boundary와 margin 사이, 1 이상이면 decision boundary 이상

  

• 이를 soft margin이라고 부름 이 때 마진을 넘는 것을 허용하기 때문에 lambda 값은 0보다 크지만 margin을 넘어가있다.

SVM with slack variables

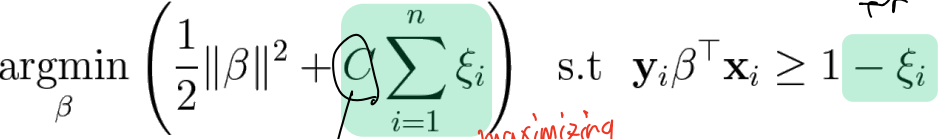
• C를 추가해서 C가 커지면 misclassification을 줄이는 것을 강조하고, 작아지면 margin을 최대화 하는 것을 강조

• 작은 C로 학습된 경우 margin의 wrong side에 들어간 것을 더 용인하고, margin이 더 커짐. 그러나 C가 큰 경우 반대로 margin이 좁아짐. ξi가 1 이상으로 큰 경우 C가 낮으면 ξi의 영향이 작고, 나머지 마진을 늘리는 부분에 집중하게 됨

Margin-based Loss

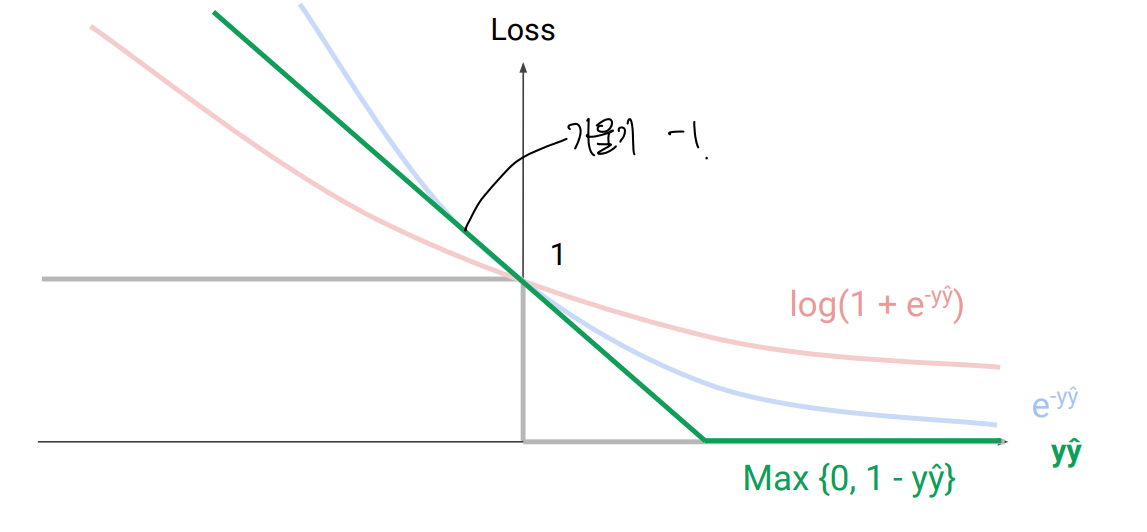
• binary 분류 문제에서, 정답과 예측값의 곱(yŷ)을 통해 loss를 결정하는 것을 Margin based loss라 함

  • 0/1 loss

  • Log loss (logistic regression에서 이걸 썼음, log (1+exp(-yŷ)) )

  • exponential loss (AdaBoost에서 이걸 썼음, exp(-yŷ) )

    • exponential한 loss를 주기 떄문에 outlier에 크게 영향을 받게 됨. → noisy data에 부적합

  • Hinge loss (support vector machine에서 L2 regularization과 함께 사용)

    

• 일반적으로 interpretable하고 output이 p(y|x) 형태로 나타나는 log loss가 많이 쓰이고 SVM에서의 hinge loss가 미분 필요없어서 많이 씀

Nonlinear SVMs and Kernels

• data가 linearly 구분 불가능한 경우가 있음.
  → kernel을 이용해서 higher dimensional space를 이용해서 linearly 구분 가능하도록 input을 변환함.

• 극단적으로, 데이터 포인트 개수만큼 차원을 높이면 이론 상으론 항상 가능한 방법

SVM은 support vector인 xi, xj(나머지는 lambda가 0이 됨)과 새로 들어오는 example x를 내적해서 분류함.

Kernel은 벡터간 내적의 일반화 개념임 (d는 d차원 polynomial 의미)

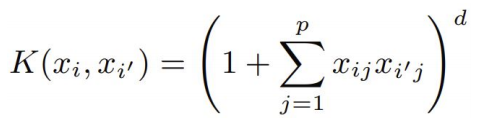
고차원으로 직접적으로 mapping하기 보다는 kernel function을 사용하는 것

정규 분포와 유사한 형태로, radial kernel도 있음

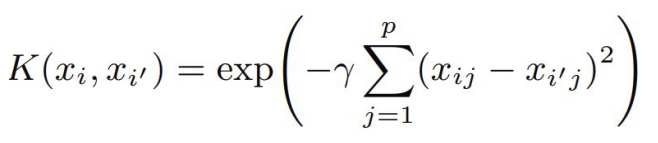
• SVM은 2개 class 분류에 맞게 디자인된 방법 → 1vsall / 1 vs1 방식의 분류까지만 가능함.

SVM vs logistic regression

• Class가 잘 분리되어 있으면 logistic regression보다 더 잘 동작함

• overlapping이 많을 수록 logistic regression이 선호되나, SVM도 어느 정도 잘 작동함

• probability를 추정하고자 할 땐 Logistic regression이 낫다.

• non linear boundary 추정에는 kernel SVM이 좋음. LR에도 kernel 쓸 수는 있으나 계산량이 과도함.

Unsupervised Learning

• data만 있고 label이 없는 경우 → 데이터만 가지고 패턴 파악, 다소 주관적일 수 있음.

Clustering

• Nearest neighbor와 마찬가지로 pairwise metric이 필요함.

• Hierarchical algorithm(bottom up, 각 개체서 부터 시작해 합쳐나감)과 partitional algorithm(top down)이 있음

Hierarchical clustering

• Agglomerative clustering: a bottom-up approach → 각 개체서 부터 시작해 합쳐나감

• threshold를 정해서 이하인 경우 합치고 아님 합치지 않는 방법

• cluster 간 거리 개념이 필요하며, closest, farthest, average 3가지 방법이 있으며, 각기 다른 결과

Partitional clustering

• K-means clustering이 있다.

• 랜덤 시작으로 cluster 중심 설정 → 가장 가까운 중심으로 cluster 할당 → 평균 지점으로 중심 이동 → 반복하다 바뀌지 않음 종료

• objective function인 J가 항상 감소하거나 같기 때문에 항상 terminate. local optimum으로의 수렴이 보장됨. J는 적어도 하나의 example이 바뀌는 경우에만 감소하고, 모든 example이 항상 assign되고, 바뀔 수 있는 경우의 수가 유한하므로 결국 수렴하는 것.

• Time complexity는 각 example을 K개 cluster마다 cluster center 재지정하는게 O(KN), cluster center를 옮기는게 O(N)으로 전체 complexity는 크지만 대부분의 경우 빠르게 수렴

• K는 증가할 경우 항상 J가 감소하므로, 일반적으로 K를 늘려가면서 elbow point를 사용함.

Dimension reduction

• data는 종종 전체 space보다 더 작은 subspace상에서 나타남 → manifold가 필요함.
• 또한 3차원 이하로 만들면 데이터를 시각화할 수 있다.

MDS(Multidimensional scaling)

• datapoint간 상대적 관계 최대한 보존하는 모델

PCA(Principal component analysis)

• MDS의 special case로, 관계를 Euclidian distance를 사용함.
• 차원을 줄일 때 원래 data의 variance를 최대한 유지하는 것과 같음. 분산 최대인 축 찾고, 거기에 orthogonal 방향으로 분산 최대인 축이 다음 선택되는 방식.

1. center를 원점으로 두고, data를 각 축 방향으로 scale 동일하게 rescaling
2. Covariance matrix를 추정하고, covariance가 0이 되도록 eigenvalue decomposition(회전 개념)
3. 대각 성분이 큰 것들만 남기고 나머지 0으로 줄이면 차원 축소됨

• PCA는 observation 에서 가장 가까운 hyperplane을 첫 vector를 정할 떄 찾게 됨. 이 때 average squared Euclidian 거리를 사용함. 반면 linear regression은 유클리드 거리를 그대로 사용하기 때문에 squared error가 항상 최소인 것은 아니다.

• 차원 개수(principal component)는 CV를 통해 결정할 수 있다.

$minimiz{e}_{{\beta }_0,\beta }[-1/n{\Sigma }_{i=1}^n{y}_i({\beta }_0+x_i^T\beta )+log(1+exp({\beta }_0+x_i^T\beta ))]+\lambda ||\beta |{|}_1$