HW_1

2022-21559 곽민준

1. α가 1, 10, 100일 때의 plot

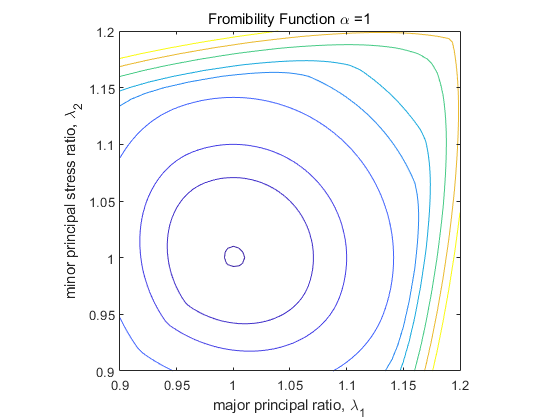
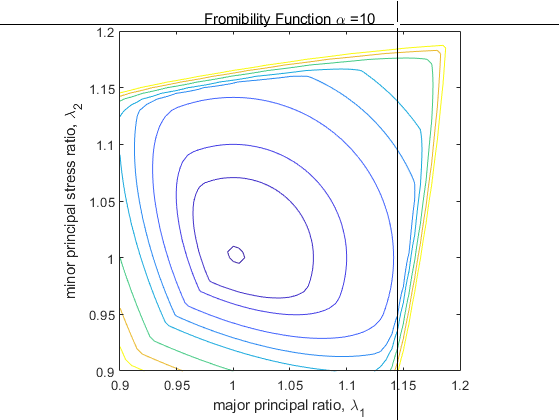
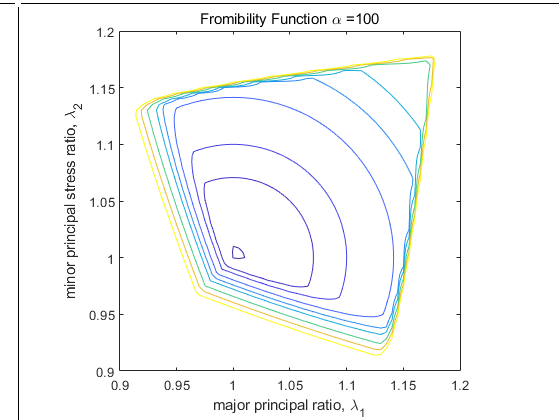
2. deformation 발생 전과 후의 plot

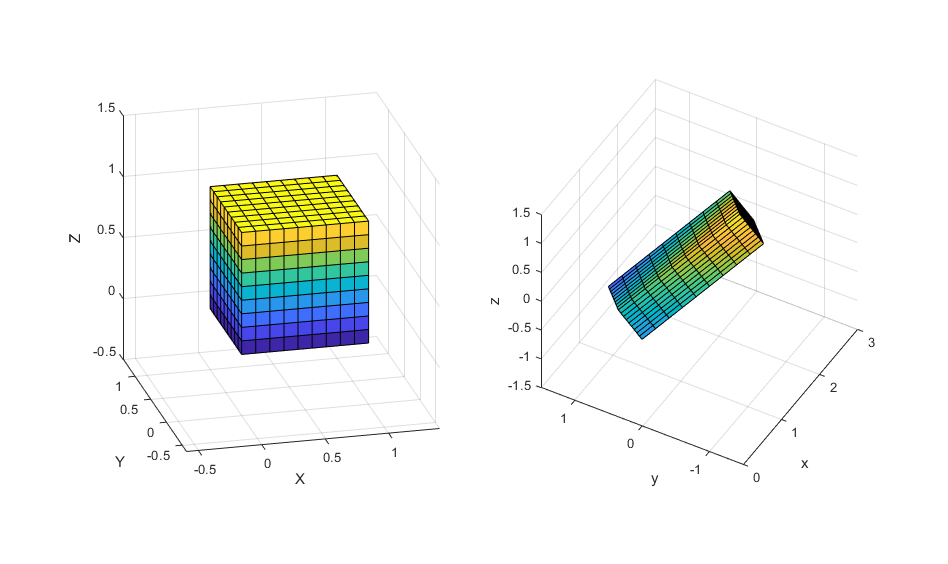
3. 1. plot3 function과 isosurface function을 이용해 구현함. plot3 function의 경우 3차원 meshgrid 생성 후, 이를 이용해 yield function을 각 grid별로 계산하며 해당 grid에서의 yield function 값과 sigma_0 값의 차가 tolerance(=1) 이하인 point를 출력하도록 함. isosurface의 경우 같은 방식의 연산을 내장 함수를 이용해 계산하도록 함.

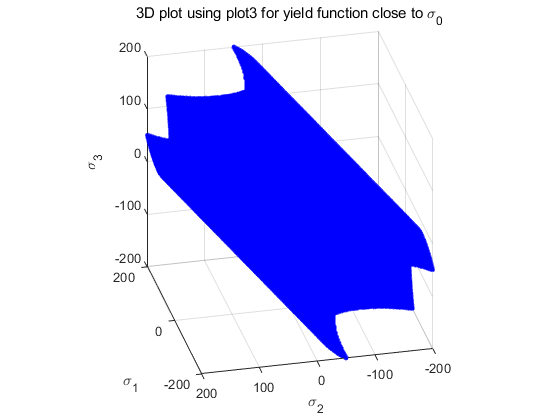
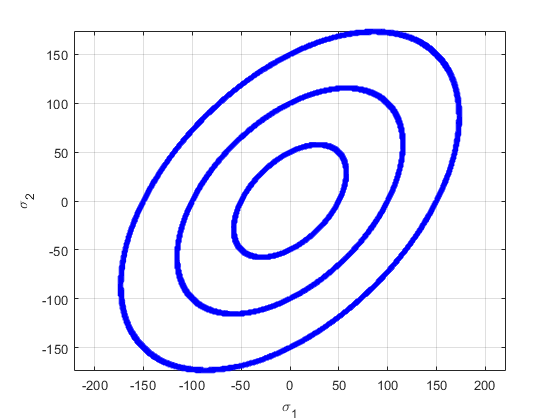
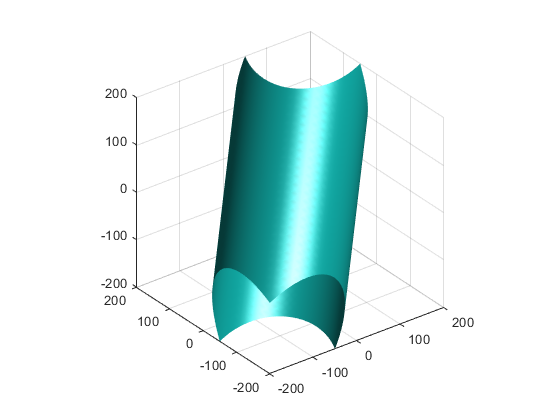3. 2) plane stress condition에서 안쪽 타원형 line부터 각각 sigma_0가 50,100,150일 때의 yield function plot임.

3번 문제에 대한 code는 아래와 같음

clc, clear

% isosurface 함수 이용

sigma0 = 150;

[sigma1, sigma2, sigma3] = meshgrid(-200:10:200, -200:10:200, -200:10:200);

yield_function = sqrt(2)/2 * sqrt((sigma1 - sigma2).^2 + (sigma2 - sigma3).^2 + (sigma3 - sigma1).^2);

figure;

isosurface(sigma1, sigma2, sigma3, yield_function, sigma0);

grid on;

axis equal;

% plot3 이용

sigma0 = 150;

[sigma1, sigma2, sigma3] = meshgrid(-200:2:200, -200:2:200, -200:2:200);

yield_function = sqrt(2)/2 * sqrt((sigma1 - sigma2).^2 + (sigma2 - sigma3).^2 + (sigma3 - sigma1).^2);

tolerance = 1;

close_to_sigma0 = abs(yield_function - sigma0) < tolerance;

x = sigma1(close_to_sigma0);

y = sigma2(close_to_sigma0);

z = sigma3(close_to_sigma0);

figure;

plot3(x, y, z, ‘b.’, ‘MarkerSize’, 10);

grid on;

axis equal;

xlabel(‘\sigma_1’);

ylabel(‘\sigma_2’);

zlabel(‘\sigma_3’);

title(‘3D plot using plot3 for yield function close to \sigma_0’);

% plane stress condition

[sigma1, sigma2] = meshgrid(-200:1:200, -200:1:200);

yield_function_plane_stress = sqrt(2)/2 * sqrt((sigma1 - sigma2).^2 + sigma2.^2 + sigma1.^2);

tolerance = 1;

close_to_sigma0 = (abs(yield_function_plane_stress - 50) < tolerance)|(abs(yield_function_plane_stress - 100) < tolerance)|(abs(yield_function_plane_stress - 150) < tolerance);

x = sigma1(close_to_sigma0);

y = sigma2(close_to_sigma0);

figure;

plot(x, y, ‘b.’, ‘MarkerSize’, 10);

grid on;

axis equal;

xlabel(‘\sigma_1’);

ylabel(‘\sigma_2’);