2022-21559 곽민준
main program
-
각 loading mode에 대해서 strain 정보 읽음
- LE11, LE22, LE12
-
elastic property 기입
- E, v
-
hardening property 기입
- f=sigma_e-sigma_0 에서, sigma_0 이 equivalent plastic strain(EPS)의 함수
- 이 프로그램에서는 linear hardening가정
- sig_Y, k: initial yield stress, coeff. of linear hardening
-
state variable initiating
- EPS: equivalent plastic strain
-
stress initiating
- plane stress인 stress=0벡터로 만듦
-
loop over the strain
-
이전 step strain과 현 step strain으로 행렬 생성하여, 전산소성역학 기말 프로젝트에 대입
→ stress updated, EPS, sig_0 출력 -
S11, S12, S22에 저장하여 다시 다음 strain으로 넘어감
-
-
모든 step 끝나면 그래프 출력
전산소성역학 기말 프로젝트
- 입력값
- E: 200Gpa, v: 0.3
- sig_Y: 200Mpa, k: 2000Mpa
- stress
- strain_prev, strain_curr
- eps
- tol1, tol2 = 1E-8, 1E-4
- E, v 값을 전산소성역학 기말 프로젝트에 대입하여 elastic stiffness matrix (C_ela) 반환
- 탄성예측 시도
-
저장된 stress에 현 step과 이전 step 사이 delta strain을 이용해 완전 탄성을 가정한 탄성 예측 stress 계산
stress = stress + C_ela*dstrain; -
stress0 (탄성예측된 stress값)으로 저장해둠
stress0 = stress
-
- 전산소성역학 기말 프로젝트 함수에 탄성예측된 stress를 대입하여 equivalent stress(sig_e) 반환
- equivalent strain을 전산소성역학 기말 프로젝트 함수에 hardening parameter들과 같이 대입하여 yield stress를 반환
- 이 equivalent stress(sig_e)값이 yield stress(sig_0)보다 작을 경우 elastic 구간이므로 별도의 계산 없이 다음 루프로 넘어가지만 더 클 경우 plastic region에 들어선 것으로, 여기부턴 뉴턴랩슨 기반의 소성 보정이 필요
-
f = sig_e - sig_0, f>0이면 소성 보정
-
f<0이면 N-R 없이 바로 다음 strain으로 loop가 넘어간다.
-
- 소성 보정을 위한 전산소성역학 기말 프로젝트사용(Euler backward scheme)
-
iteration을 통해 delta lambda(plastic multiplier) 값을 보정
-
d(delta lambda) 값을 더해가면서 dlam값 update, stress도 마찬가지로 update
-
만약 residual값과 f값이 tolerance보다 작으면 yield function 위에 있다고 판단, loop 종료
-
- 소성 보정이 완료된 delta lambda값을 eps에 update
- 다음 step으로 넘어감
전산소성역학 기말 프로젝트
- 스칼라값 E, v값을 받아 elastic stiffness matrix(C_ela) 반환
전산소성역학 기말 프로젝트
-
stress [sigma_11;sigma_22;sigma_12]를 받아서 equivalent stress 반환
-
a는 yield function 위에서의 normal 방향이며, gradient of yield function
전산소성역학 기말 프로젝트
- equivalent plastic strain(eps), coeff. of linear hardening(k), initial yield stress(sig_Y)를 받아 yield stress(sig_0) 반환
- 여기선 linear hardening을 사용
전산소성역학 기말 프로젝트
-
TODO: delta(delta lambda), delta stress 계산
-
4 Unknowns: delta lambda(1 scalar unknown), stress at C(3 unknown values on the yield surface)
-
4 equations
-
r vector에서 3equation, f값에서 1 equation
강의자료의 경우 3D(7x7)였으나 2D(4x4)로 수정하여 사용하였음 -
simplified matrix equation
$( \mathbf{r}=\boldsymbol{\sigma}_{C}-\left(\boldsymbol{\sigma}_{B}-\Delta \lambda \mathbf{C} \mathbf{a}_{C}\right)=0)$
-
-
matrix 각 성분 계산
-
upper left
-
r에서 trial stress(sigma_B)는 fixed value이므로,
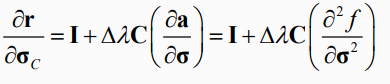
-
-
upper right
-
lower left
- a의 definition에서,
-
lower right
-
Von Mises에서 delta lambda = epsilon_ps 이므로,
-
A’값은 이 코드에선 k값으로 사용됨
-
-
-
update를 위한 delta 값들 계산
-
단순화를 위해, Q matrix를 정의
-
아래 equation을 풀어 delta값 계산
0=\left(\begin{array}{l}\mathbf{r} \\ f\end{array}\right) +\left(\begin{array}{l}\Delta \mathbf{r} \\ \Delta f\end{array}\right)\\ \\ 0=\left(\begin{array}{l}\mathbf{r} \\ f\end{array}\right)+\left[\begin{array}{cc}\frac{\partial \mathbf{r}}{\partial \boldsymbol{\sigma}} & \frac{\partial \mathbf{r}}{\partial \Delta \lambda} \\ \left(\frac{\partial f}{\partial \boldsymbol{\sigma}}\right)^{T} & \frac{\partial f}{\partial \Delta \lambda}\end{array}\right]\left(\begin{array}{c}\Delta \boldsymbol{\sigma} \\ \Delta^{2} \lambda\end{array}\right)\\ \left[\begin{array}{cc}
-
-
계산된 delta 값을 update 후 f, r값 tolerance와 비교하여 수렴 여부를 파악
결과 분석
※ 각 case에서 왼쪽 위에서부터 각각 11, 22, 12 방향에 대하여 stress를 코드를 통한 계산한 값을 y, 아바쿠스로 추출된 데이터를 x로 하여 plot한 것임
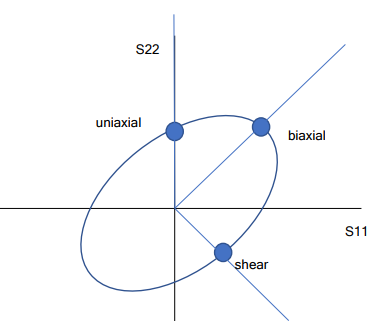
- plots
-
Uniaxial
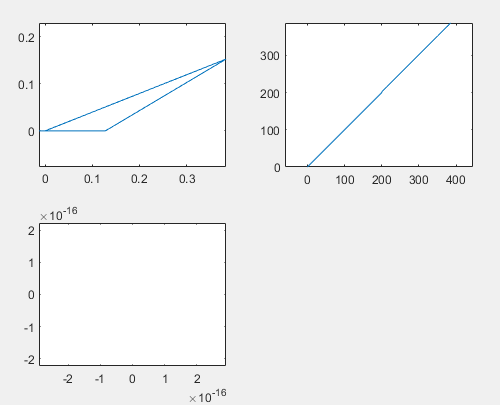
-
Biaxial
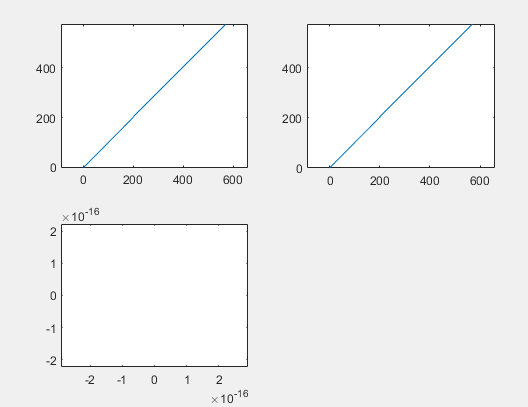
-
Shear
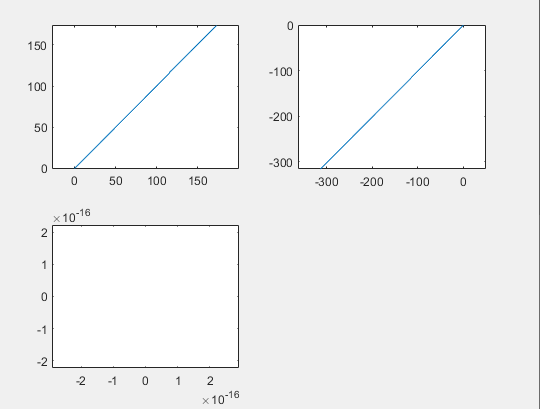
-
- 세 케이스 모두 정상적으로 수렴하였으며, 데이터를 보았을 때 모든 mode에서 코드를 통해 도출된 stress값과 레퍼런스 아바쿠스 stress 값이 대체로 일치하는 것을 확인할 수 있다. uniaxial의 경우 S11에서 약간 값이 튀긴 했으나 거의 0에 가까운 값이 도출되었으며, 이는 아바쿠스 데이터와도 거의 유사하다.
- iteration의 경우 total iteration update 코드를 추가하여 확인한 결과 uniaxial에서 총 555번, biaxial의 경우 600번, shear의 경우 550번으로 집계되었다.
- 효율 평가를 위해 strain increment를 현재 값에서 2배로 하여 계산했을 때 total iteration 횟수는 더 줄어든 318번으로 집계되었다.