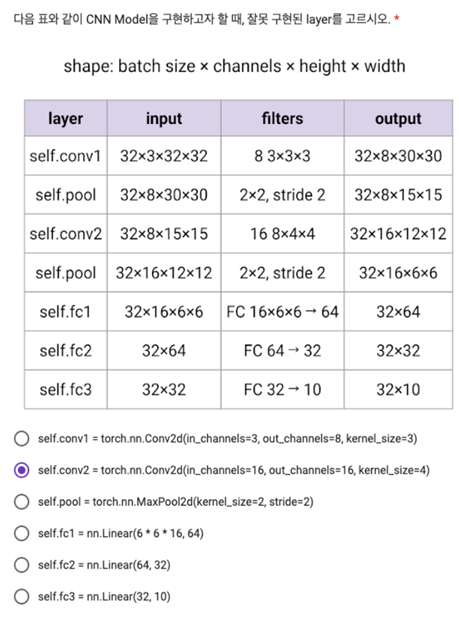
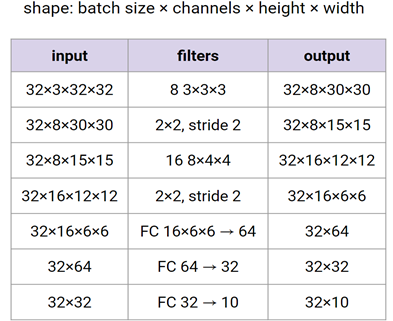
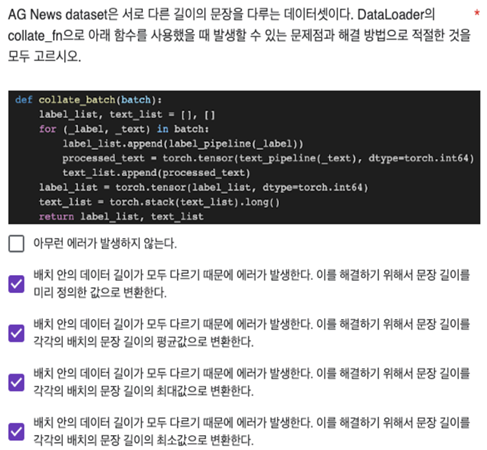
linear classifier를 사용하면 classify 불가능한 nonlinear case엔 적용 불가
→ input을 표현할 수 있는 feature를 추출한 뒤, feature space에서는 linearly separable하다면 linear classifier를 사용할 수 있다.
→ 이미지에서 feature 를 추출하고, 이를 이용해 label y를 추측함. 이 때 feature로부터 y를 추측하는 함수만 학습하게 됨.
Neural networks
perceptron을 사용하기 위해 multiple neuron을 사용하고, single layer보다 multilayer를 사용함
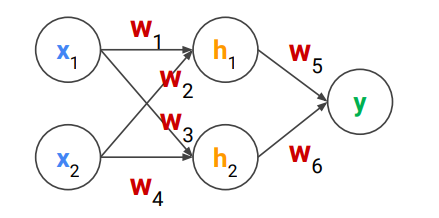
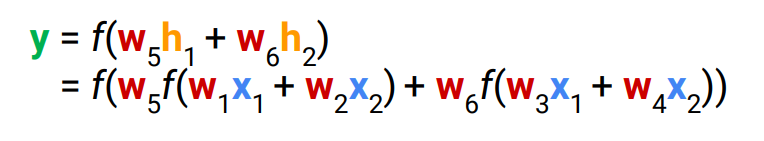
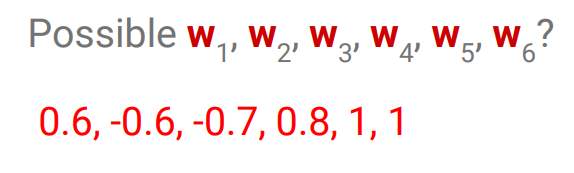
multilayer에서, W2(W1(x))이면 결국 linear하게 나오기 때문에, non linearity를 추가하고자 activation function을 사용함. → sigmoid, tanh, ReLU
여기서도 Gradient Descent를 쓸 수 있고, 이 경우 각 weight에 대한 loss의 gradient가 필요함.
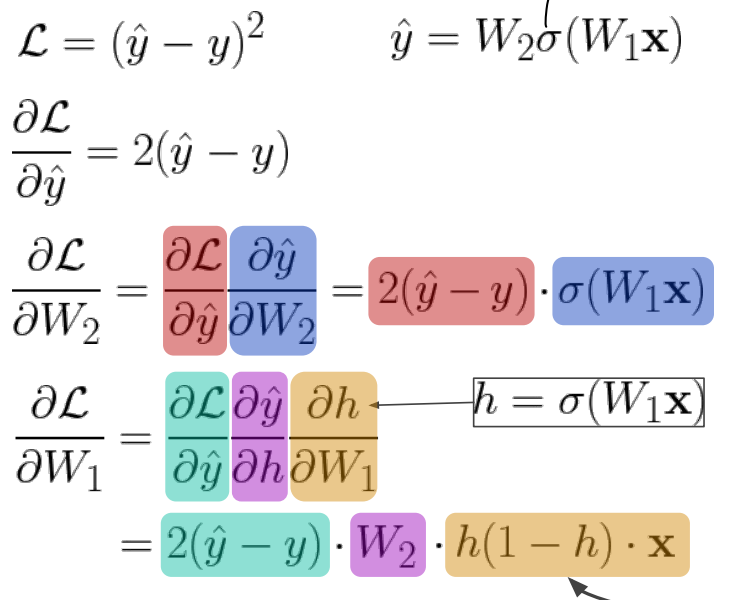
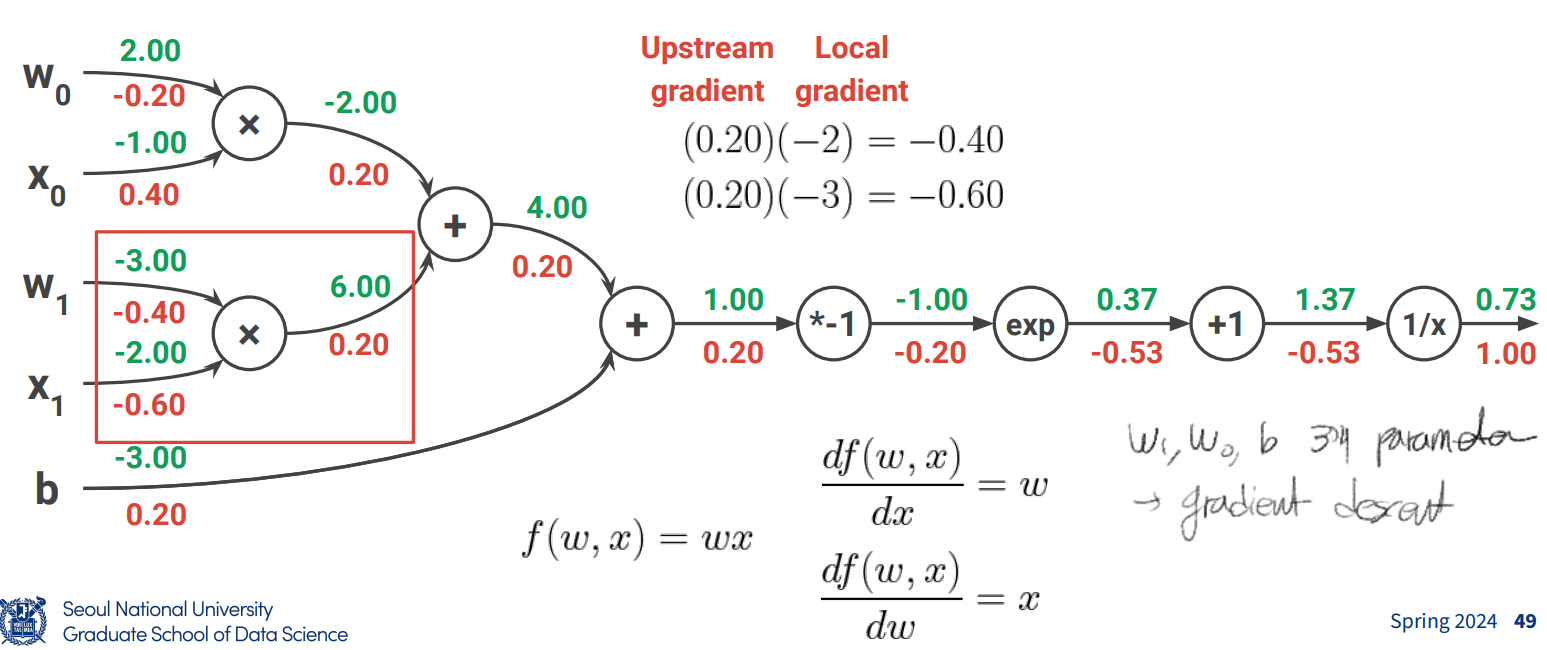
Backpropagation: Computing Gradients
계산은 forward pass로 이루어지고, parameter 수정은 back propagation으로 이루어짐
해당 step까지 forward pass로 계산된 z값과, 직전 calculation operator를 이용해 back propagation
- upstream gradient
- 직전 operator 미분한 operator 계산 후, 해당 operator에 들어오기 전 forward pass값을 대입해 local gradient 계산
- 둘이 곱해 back propagation
- pattern of gate
- add gate: 그냥 분배
- mul gate: swap multiplier
- copy gate: gradient adder
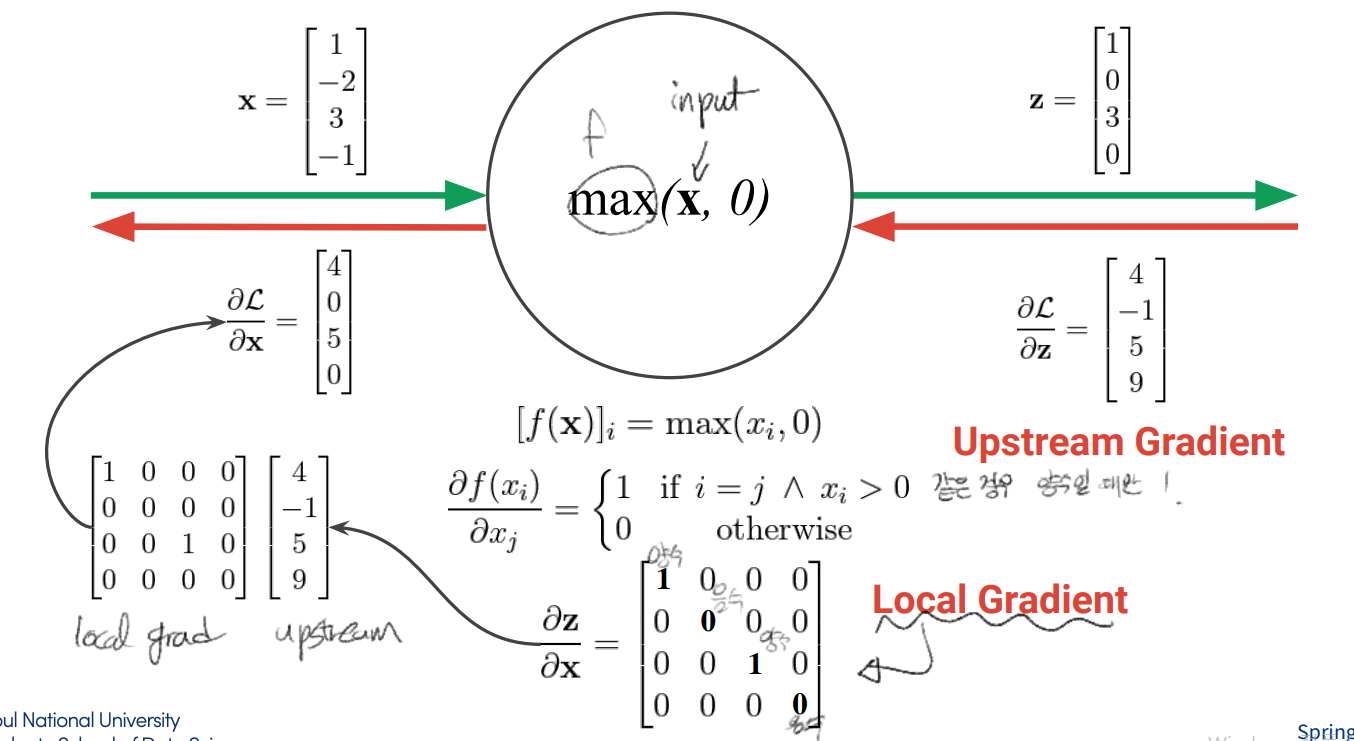
- max gate: 더 큰 쪽만 그대로 가고, 작은 쪽은 0으로 감
Back propagation with Vectors and Matrices
- 스칼라 y가 스칼라 x에서 나온다면 기존의 미분이 성립
- 스칼라 y가 벡터 x로 부터 도출되는 경우, dydx도 x와 동일한 차원 가지고, 각 i번째 성분이 xi에 대한 y의 미분이 됨
- 벡터 y가 벡터 x로부터 도출되는 경우 dydx는 2차원 matrix형태인 jacobian matrix
back propagation 시 variable에 대한 gradient는 original variable과 동일한 dimension을 가짐. 이는 loss 자체는 scalar이기 때문 (2의 케이스)
back propagation 방법
-
upstream gradient
-
operator에 대해서, input vector의 각 component에 대해 미분
-
local gradient * upstream gradient
Fully connected layer의 경우 모든 input value로 부터, 모든 output value를 연결짓는 모델임.
→ any output value가 any input value에 영향을 받게 됨.
Convolutional neural network은 filter를 사용해, inner product 방식으로 target object를 찾게 됨.
main assumption
-
Spatial locality: 특정 위치 주변 픽셀들로만 판단
-
Positional invariance: 위치와 상관없이 찾을 수 있어야함.
Convolutional Layer
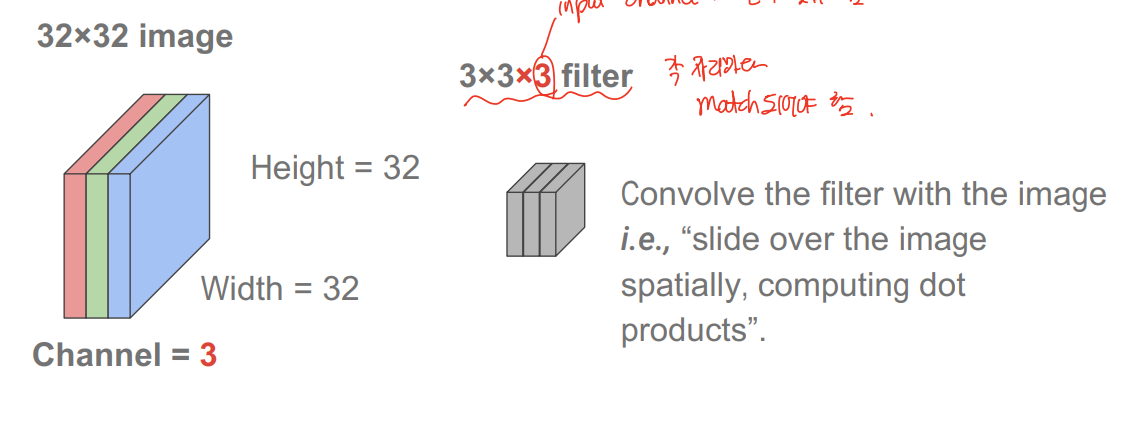
input channel과 filter channel은 동일하게 맞춰야한다.
위의 경우 333=27에 bias까지 총 28개의 convolution 결과가 각 pixel에 result로 더해짐.
그 결과 activation map으로 30301의 size로 output
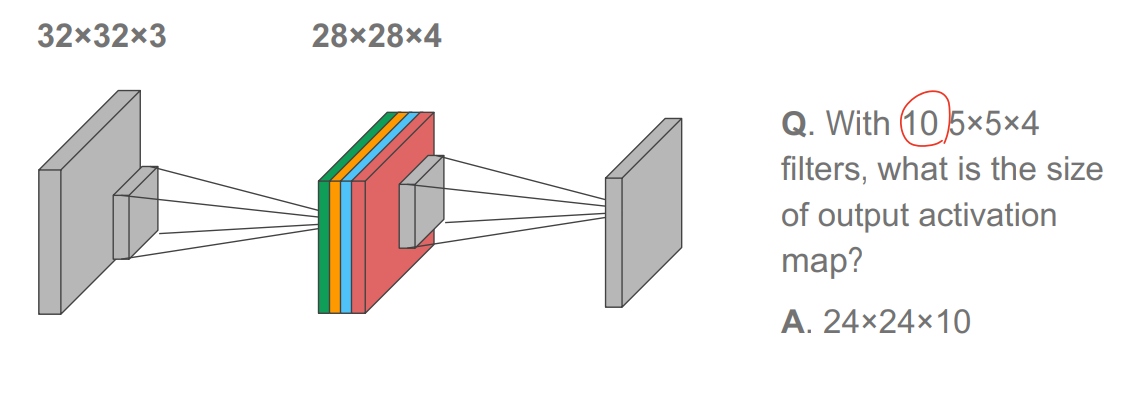
경우에 따라 서로 다른 feature 탐색을 위해 서로 다른 filter를 한번에 여러개 사용하는 경우도 있음. 이 경우 filter 개수만큼 곱해지게 됨. 아래 케이스의 경우 4개의 5x5x3 필터를 사용한 케이스
nested convolution layer 사용 시 문제점
- filter 크기가 커질 수록 activation map은 크기가 급격하게 감소
- padding 사용
- filter 중심이 1,1로 갈 수 있게 맞추며 P=(F-1)/2
- image 가 너무 클 경우 computation cost 증가
-
stride를 사용함.
-
output size = (N-F+2P)/stride +1, N은 input image, F는 filter, P는 padding 두께
정수로 떨어져야 적합함.
-
예시
input volume 32x32x3에 10개의 5x5x3 filter with stride 1, pad 2
→ output size 32x32x10이고, number of parameter는 여기에 filter 수인 (5x5x3+1)x10=760
→ CF) FC일 경우 (32x32x10)x(32x32x3+1) (input output volume에 bias까지)
input volume 32x32x3에 6개의 1x1x3 filter with stride1, pad 0
→ output size는 32x32x6, parameter 6(1x1x3+1)
정리하면
output size
- width = (W-F+2P)/S+1
- Height = (H-F+2P)/S+1
Number of parameters
K(F^2C+1) (c는 channel 수, k는 filter 수, F는 filter size)
pooling layer
image 크기 축소 개념, downsampling(more manageable) and denoising(controlling overfitting)
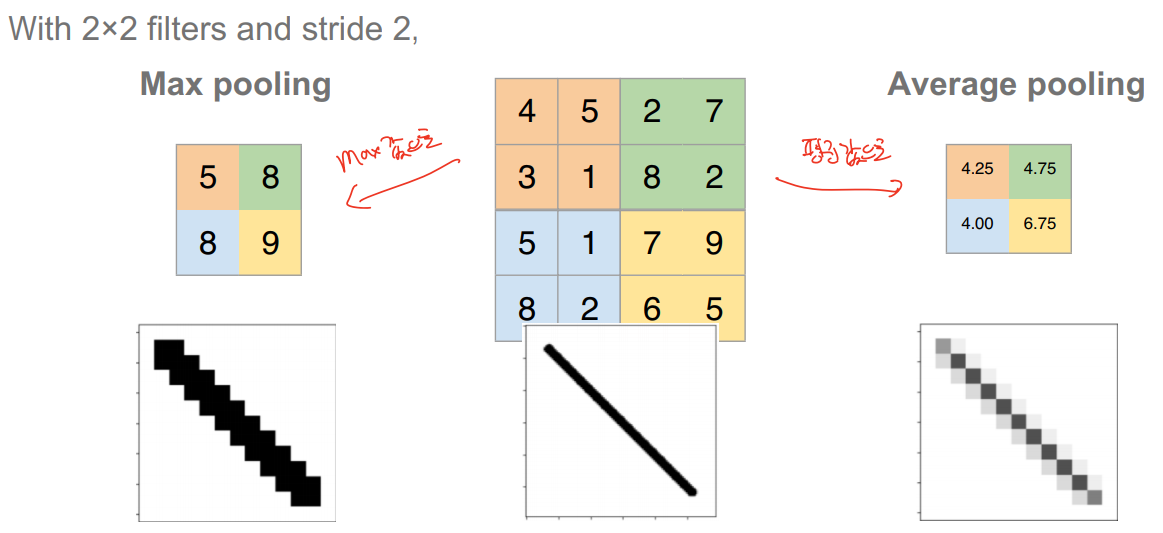
output size H’W’C일 때
W’ = (W - F) / S + 1
H’ = (H - F) / S
number of parameters: 0 (no learning happens)
<Training Neural Networks 1>
Activation functions
nonlinearity 도입하기 위해 activation function을 사용함
sigmoid의 경우 saturated neuron에서 killing gradient 문제가 있고, 이는 tanh도 마찬가지.
→ back propagation시 upstream gradient에 activation function gradient가 곱해져 나아가는데, 이 activation function의 gradient가 쉽게 0이 되어, 이후 gradient도 계속 0이 됨.
추가적으로 sigmoid의 경우 output이 not zero centered
→ activation function의 gradient가 gradient update를 할 때 부호가 바뀌지 않음.
Data Preprocessing & Augmentation
translation, rotation, stretching, color jittering 등 하나의 data에 여러 전처리를 거쳐 학습
Weight initialization
neural network에서 weight를 initialization을 할 때 대충 정규분포에 맞게 값 추출 후 적당한 수를 곱해서 사용하면 shallow NN에선 문제가 안되지만 deep neural network에서 activation은 layer를 거침에 따라 문제 발생. 곱해진 수가 너무 작으면 activation 이 점차 shrink, 너무 크면 마찬가지로 learning 발생하지 않음.
Xavier Initialization
initialization 시 정규분포로 뽑은 값을 input dimension의 크기를 루트 씌운 값으로 나누면 어느 정도 해결된다. → input과 output variance를 맞춰줌., W와 x 가 iid를 만족한다는 가정 하에서 성립
Weight initialization of ReLU
마찬가지로 ReLU도 x가 0에 가까워짐에 따라 모든 gradient가 0에 가까워지고, learning이 발생하지 못함. 따라서 initialization이 중요함. → Kaiming/MSRA Initialization, 2/d_in에 루트 씌운값을 곱해줌. (아까 값에서 2가 곱해짐.)
Learning rate scheduling
learning rate가 너무 작으면 비효율적이고, 느리게 수렴. 너무 크면 발산하거나, 미세한 조정이 어려워져 global minimum에 도달하지 못할 수 있음. 모델마다 최적 값이 바뀌므로 항상 찾아주는게 좋음.
learning rate decay
처음엔 큰 lr을 쓰고 나중엔 점차 줄여줌. 학습이 진행될수록 미세한 조정이 필요한 경우가 많음.
<Training Neural Networks 2>
Deep NN에서 overfitting 방지 위한 regularization method
- Weight decay
- weight 에 대한 penalty term을 추가해서 ridge, lasso 사용 가능
- Early stopping
- validation set을 이용해서 validation set에서 overfit 발생 시 stop
- Drop out
-
forward pass에서 랜덤하게 특정 뉴런 0으로 설정
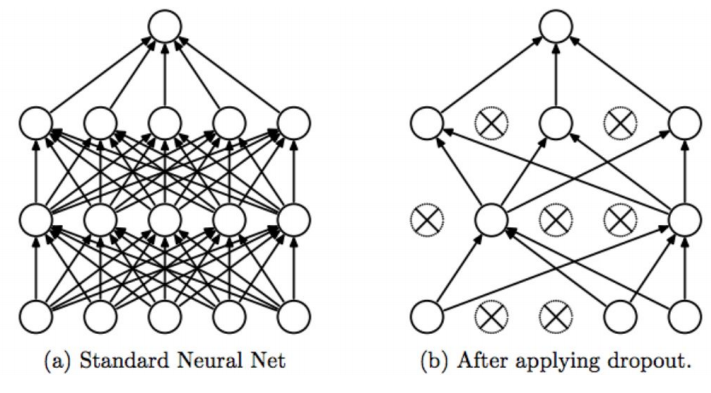
-
이를 학습 시 마다 랜덤하게 드랍해서 진행
-
Optimization beyond SGD
SGD는 각 축 방향으로 gradient 차이가 매우 클 경우 jittering이 발생하여 느리게 진행
saddle point나 local minimum에서 멈출 수 있음
gradient가 mini batch로 계산되므로 정확하지 않을 수 있음. 그러나 메모리 문제로 큰 데이터가 들어와도 배치 크기에는 한계가 존재하게 됨.
SGD+ momentum
일종의 관성을 부여해서 작동함.
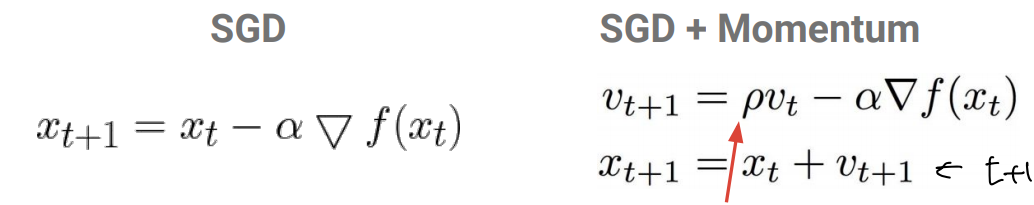
AdaGrad
learning rate을 element, dimension별로 따로 설정해서 steep direction은 느리게, flat direction은 가속화되게 함. gradient를 divider로 나누며, divider는 gradient의 누적 합이 됨.
RMSProp
leaky AdaGrad이며, Adagrad는 지속적으로 누적되는 방식이라 step 누적 시 learning rate가 크게 감소함. 따라서 decay rate을 도입해 사용하게 됨. 이 떄 old value와 새 gradient 분율 합을 1로 유지해서 conservatively updated
Adam
RMSProp과 SGD+momentum의 결합 방식.
First vs second order optimization
2nd order를 쓰면 더 정확하고 빠른 수렴이 가능하지만, quadratic approximation에서 더 많은 calculation cost 발생
Batch normalization
layer 여러 층일 때 첫 번째 layer는 input data를 data processing(zero center, unit variance) 처리가 가능한데, intermediate layer는 어떻게?
→ 해당 layer에서 aactivation 에 대한 batch에서 마찬가지로 처리하면 됨.
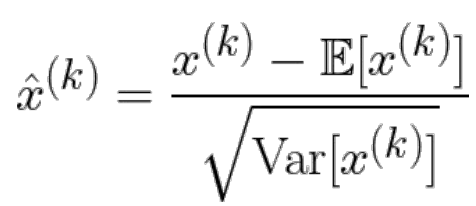
→ 기댓값과 variance에 대한 예측 필요
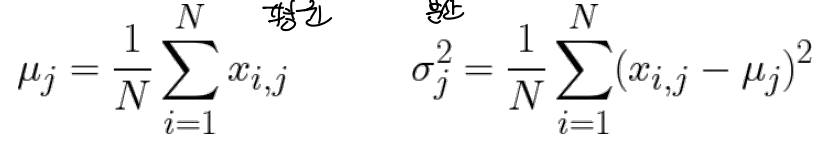
N은 data 개수, D는 data의 dimension, j가 각 dimension
→ μ,σ,x의 dimension = D, D, NxD
data processing을 위해 activation function에 normalized value를 넣어주어야함. 그러나 단순히 각 input을 normalizing하느건 각 layer가 표현할 수 있는 것들에 영향을 주고 너무 rigid하게 될 수 있어, 추가적인 capacity가 필요함.
→ 추가 parameter를 써서, 이를 복원할 수 있게 함.
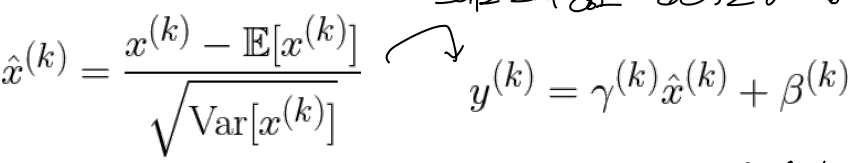
gamma가 분산 역할, beta가 평균 역할이며, 각 값은 학습되는 parameter임.
학습할 때는 batch size에 맞게 normalizing하더라도, 테스트할 때는 이게 불가능함. 따라서 batch size=1일 때에도 굴러가도록 해야 함. 또 평균 및 분산값을 저장해뒀다가 테스트 떄 써야 위의 전략 사용 가능함.
→ batch normalization
<Sequential Data & Recurrent Neural Networks I>
input과 output 길이가 정해져 있지 않으면서, sequence인 경우
Word Embedding
단어를 vector로 표현해서 관련성 높은 단어들은 비슷한 공간 상 위치에 있도록 함.
- Word2vec
- neighboring word로 부터 current word를 예측하거나 current one으로부터 surrounding word를 예측 → 자주 같이 쓰이는 단어들로부터 단어 의미가 결정됨.
- GloVe
- 벡터로 표현.
Recurrent Neural Networks for Sequence Classification (Many-to-one)
단어들 각각의 의미만 가지고 전체 문장 유추하는데에는 한계가 있음.
1st try: Convolutional NN
단어들을 Word2vec이나 Glove로 embed시키고, convolutional filter를 사용해 순서에서 나타나는 pattern을 학습하도록 함. → input size가 fixed 문제 발생.
new idea: encoder
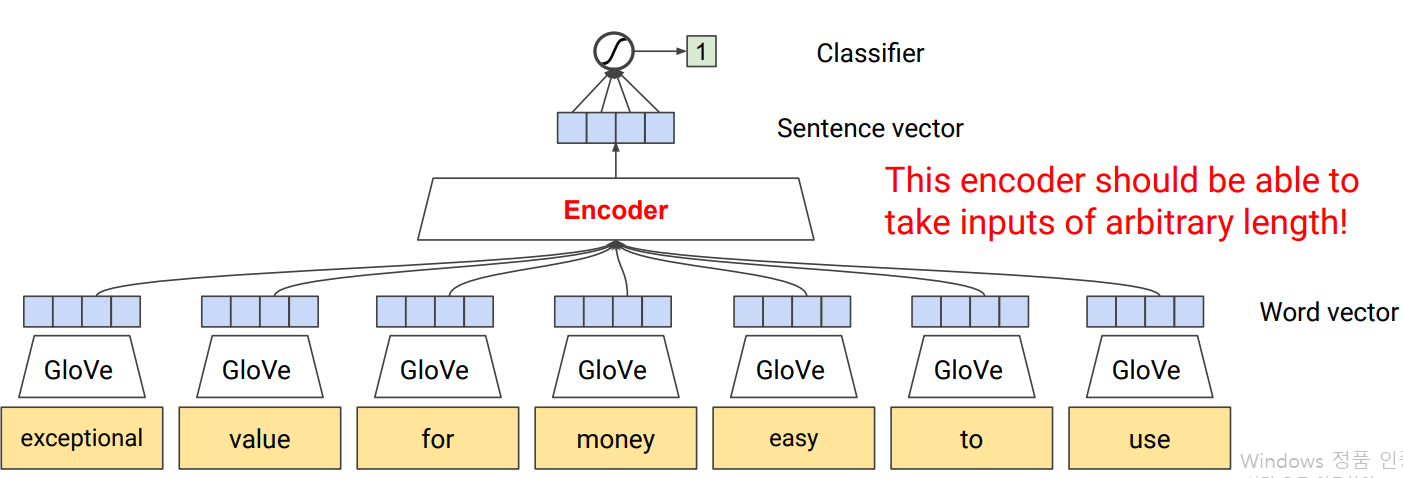
entire sequence을 input으로 받아서 encoding 시키는 방식
Recurrent NN
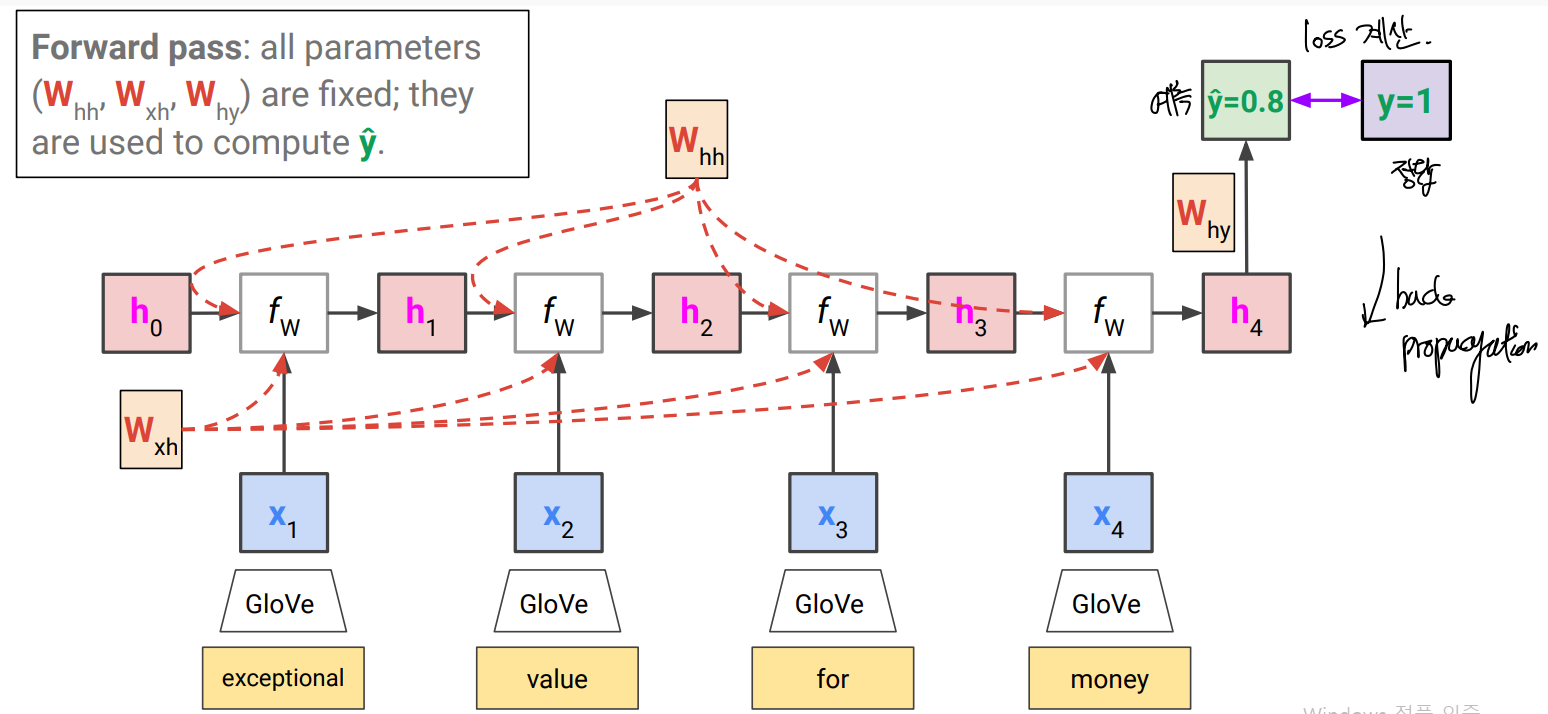
input sequence를 하나씩 읽어내고, 해당 input까지 읽어낸 의미를 나타내는 internal state를 유지함. 그리고 각 step마다 새 internal state가 old state와 input으로부터 정해짐.
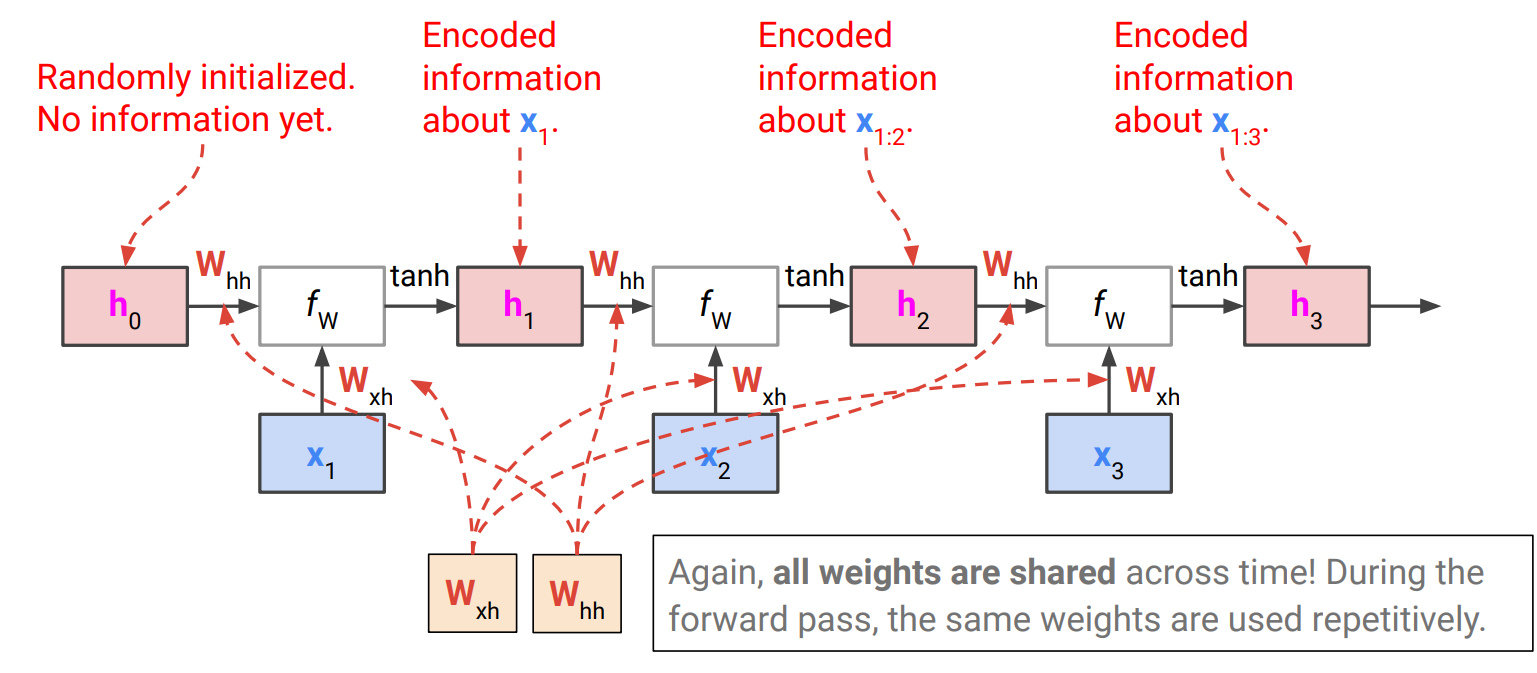
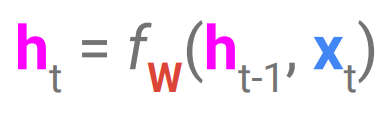

이 때, 모든 step에서 같은 f와 W가 사용된다. 그렇지 않을 경우 arbitrary length에서 문제가 됨
각 RNN cell 안에선, fully connected layer에서 f(x)=σ(Wx)로 썼던 것과 같은 방식으로 2개의 input variable에 대한 각 weight가 필요하므로 Whh, Wxh 2개를 선형 조합해서 사용하고, activation function (여기선 tanh)을 거쳐 nonlinarity를 완성
→ 전체 input sequence가 encoding을 마치면 classifier나 regressor 등을 사용하여 encoding을 final output으로 mapping하도록 함.

back propagation
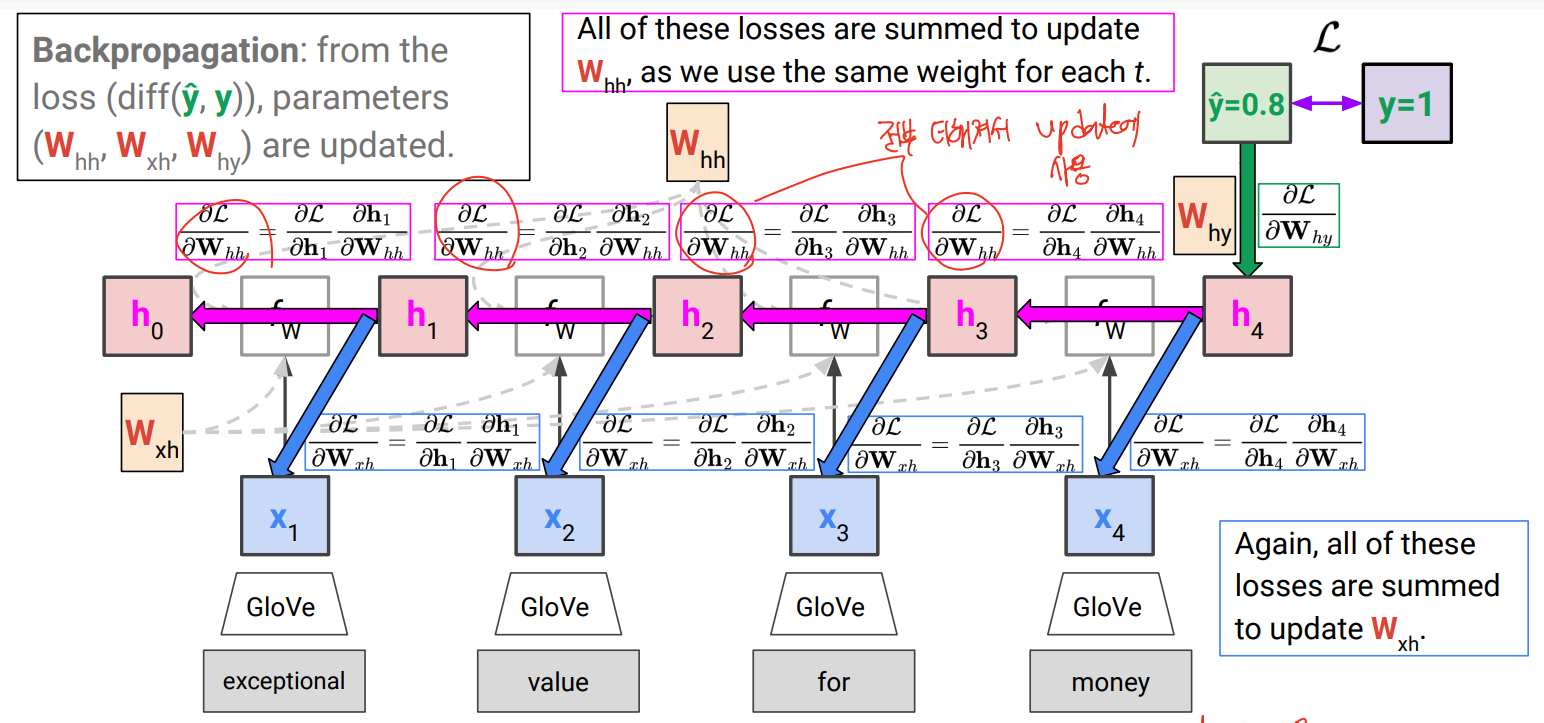
각 step에서 gradient가 생기고, 이를 모두 더해서 update에 사용함. (3개의 weight 있음)
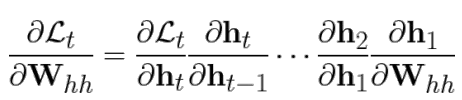
Recurrent Neural Networks for Sequence Classification (Many-to-Many)
RNN for language model
output도 word level에서 진행하게 됨. → 이전 단어들의 sequence로 부터 vocabulary 내의 단어 중 다음 position에 올 확률을 단어 레벨에서 추측하는 것. → multiclass classification problem
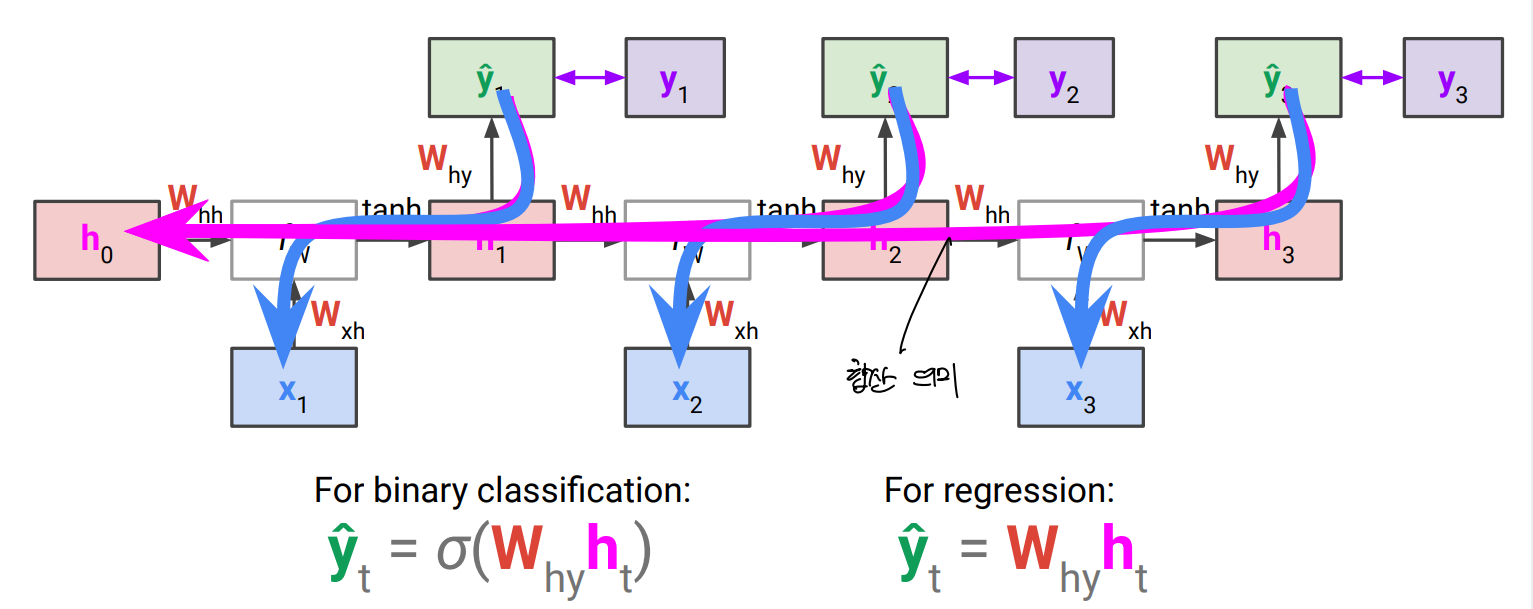
각 step에서 y를 추측하게 되며, back propagation도 이루어짐.
hidden layer를 1층 이상으로 쌓을 수도 있다.
Trade-offs of RNN
- 장점
- input 길이에 영향 받지 않고, input이 늘어나도 model size가 늘지 않음.
- 이전 step의 information을 해당 step의 학습에 반영할 수 있음.
- 같은 weight가 계속 사용됨
- 단점
-
sequential 연산으로 parallelization이 불가능하여 느림
-
학습 시 vanishing gradient 문제가 발생하여 long-range dependency를 갖는 모델을 만들기 어려움 → LSTM/GRU로 해결 가능
-
서로 다른 길이를 갖는 input/output case를 다루기 힘들다. → seq2seq model 사용
-
<Recurrent Neural Networks II (LSTMs & Seq2seq Models)>
t번째 step에서 RNN backpropagation 시 아래와 같이 gradient 계산될 때, Whh가 t-1번 곱해지게 됨.
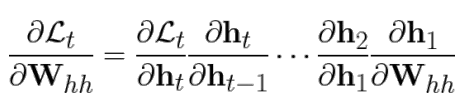
따라서 weight 값에서 값이 1보다 큰 경우 exploding하고 , 1보다 작으면 vanishing 하는 문제가 생겨버림
RNN은 input sequence길이가 depth역할을 하기 때문에 이런 문제가 CNN보다 더 많이 발생함.
Exploding gradient 문제
각 gradient를 maximum value로 clipping함으로써 해결함. 어느 정도 커지면 잘라내고, 방향은 유지하도록 함.
→ exploding은 해결되었지만 shrinking은 해결 못하고, later input에서의 loss는 초기 step까지 쉽게 반영되지 못하는 문제, long range dependency가 떨어지는 문제
Towards modeling longer dependence
vanishing 문제는 BP 시 FC를 지나가기 때문에 발생함.
vanishing 문제를 해결하기 위해 새 hidden state인 cell state를 highway처럼 FC layer 위에 추가함.
→ long term으로 저장할 수 있는 새로운 cell이 추가됨 forward 시 FC, tanh 지난 output이 Ct와 더해져 다시 tanh 거쳐 ht가 됨.
vanishing 문제를 완전히 차단하는건 아니지만 어느 정도 잘 해결해줌
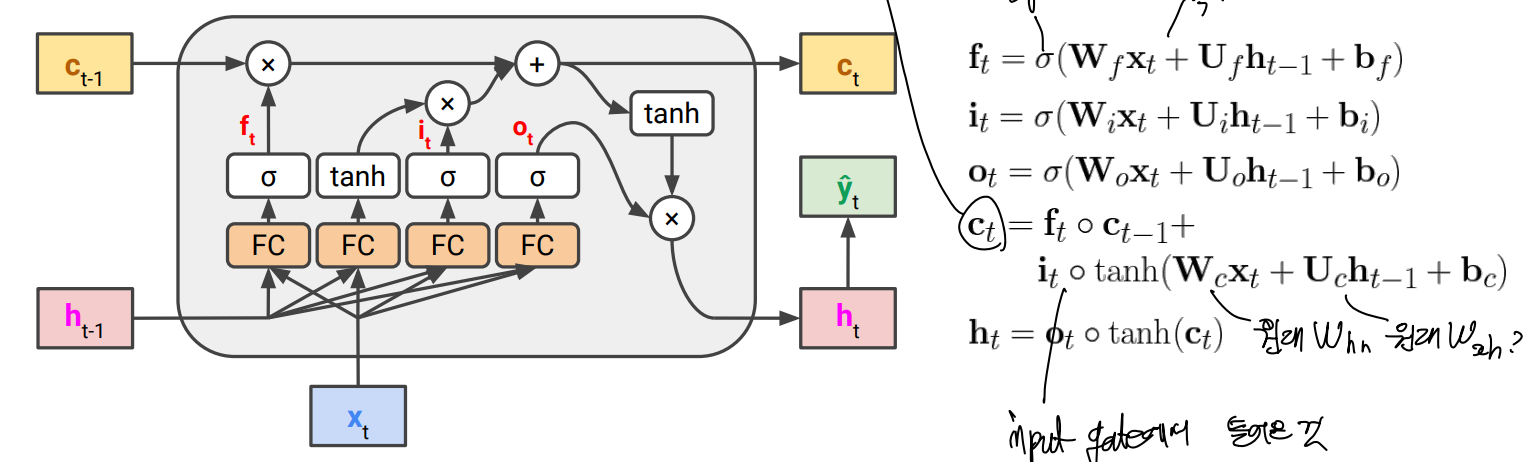
gate
- forget gate
- 한 문장이 끝나면 이전 문장 정보 지우는 등 forget 과정이 필요함. 이를 위해 별도의 FC를 학습하게 되며, sigmoid 거친 결과가 0에 가까우면 Ct-1 정보를 많이 줄이는 방식
- input gate
- input으로 읽은 값이 long term memory에 들어갈 내용인지 아닌지를 결정할 수 있도록 하는 별도의 FC 학습
- output gate
-
ct-1에 의한 정보가 ht에 얼마나 영향을 미칠지도 output gate을 통해 조절함.
-
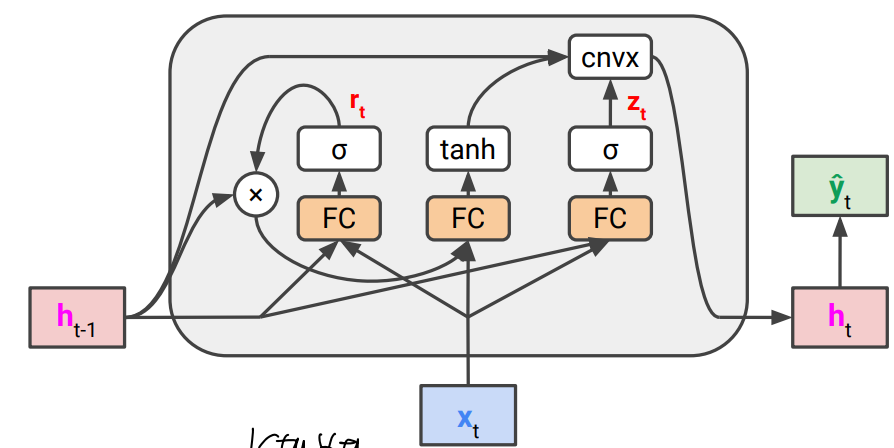
Gated Recurrent Units (GRU)
LSTM과 다르게 추가적인 cell state가 없고 lstm보다 parameter가 더 적어서 계산이 더 빠르다.
이전 hidden state와 input으로부터 계산된 another output을 convex combination을 사용해서 gradient highway 제공
Sequence-to-Sequence (seq2seq) Models
기계 번역 등에 사용되는 모델
언어 변경의 경우 일대일 대응이 되지 않는 문제가 있어서, sequence 상에서 하나의 단어 input으로 대응되는 단어 output 도출에는 한계가 존재한다. 또는 어순이 반대여서 해당 sequence까지의 정보로 번역이 불가능해지는 경우가 생김.
이를 위해 기존 RNN에서 output 없이 encoding을 진행함. 이후 decoder를 제작하여 사용
→ Many-to-one(single vector) as encoder, then one-to-many as decoder.
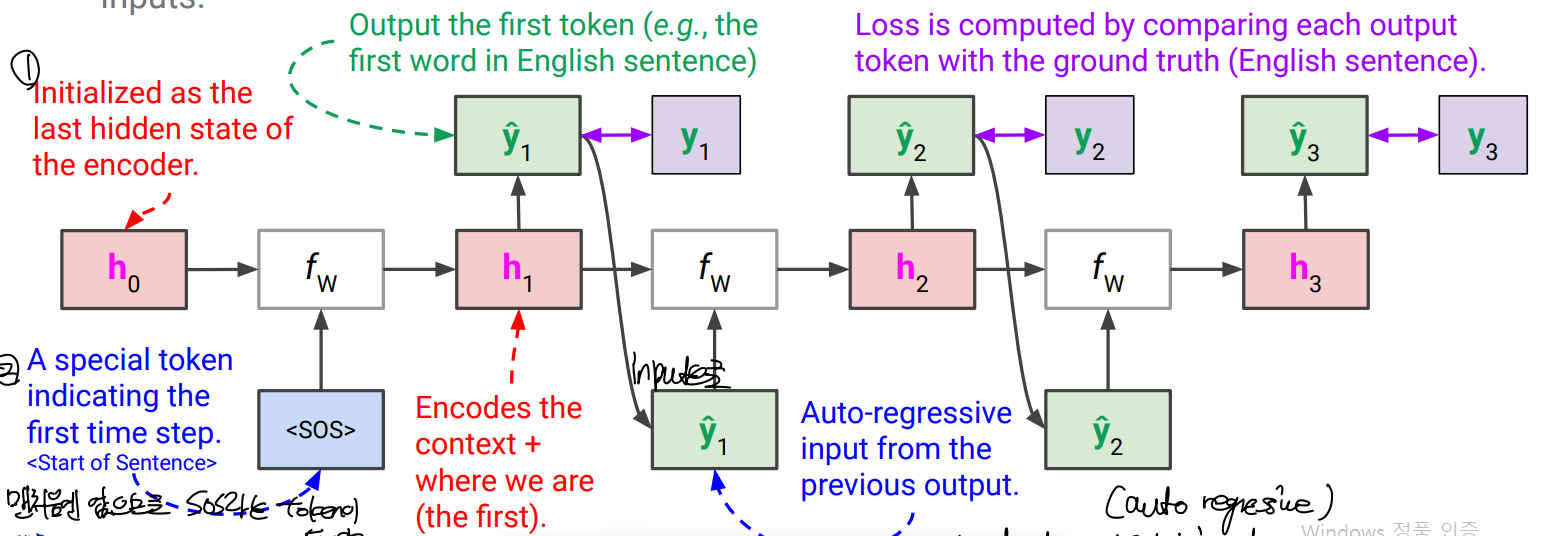
- encoder의 last hidden state로 initialize, 1st input으로 special token 삽입
- decoder 각 step에서 출력값이 그 다음 step에서의 input 값으로 들어가게 함. (auto regressive input) 그러나 학습의 경우 틀린 input이 뒤 step까지 영향을 주게 되므로 학습에선 정답 y값을 다음 step의 input으로 사용함. (실제 사용 시에는 y hat이 들어감)
- loss는 각 y값과 비교해서 계산
<Attention Mechanism & Transformers I>
LSTM과 GRU가 여전히 long term에서 information loss가 발생함.
→ attention에서는 해당 query(decoder step)와 input에서 h1, h2,…간의 relevance를 계산해서 weight 곱해 합산
Query(context), key-value pair를 input으로 받아 value의 weighted average인 attention value를 출력하는 attention function을 사용, 각 weight는 query와 corresponding key간의 relevance에 비례함.
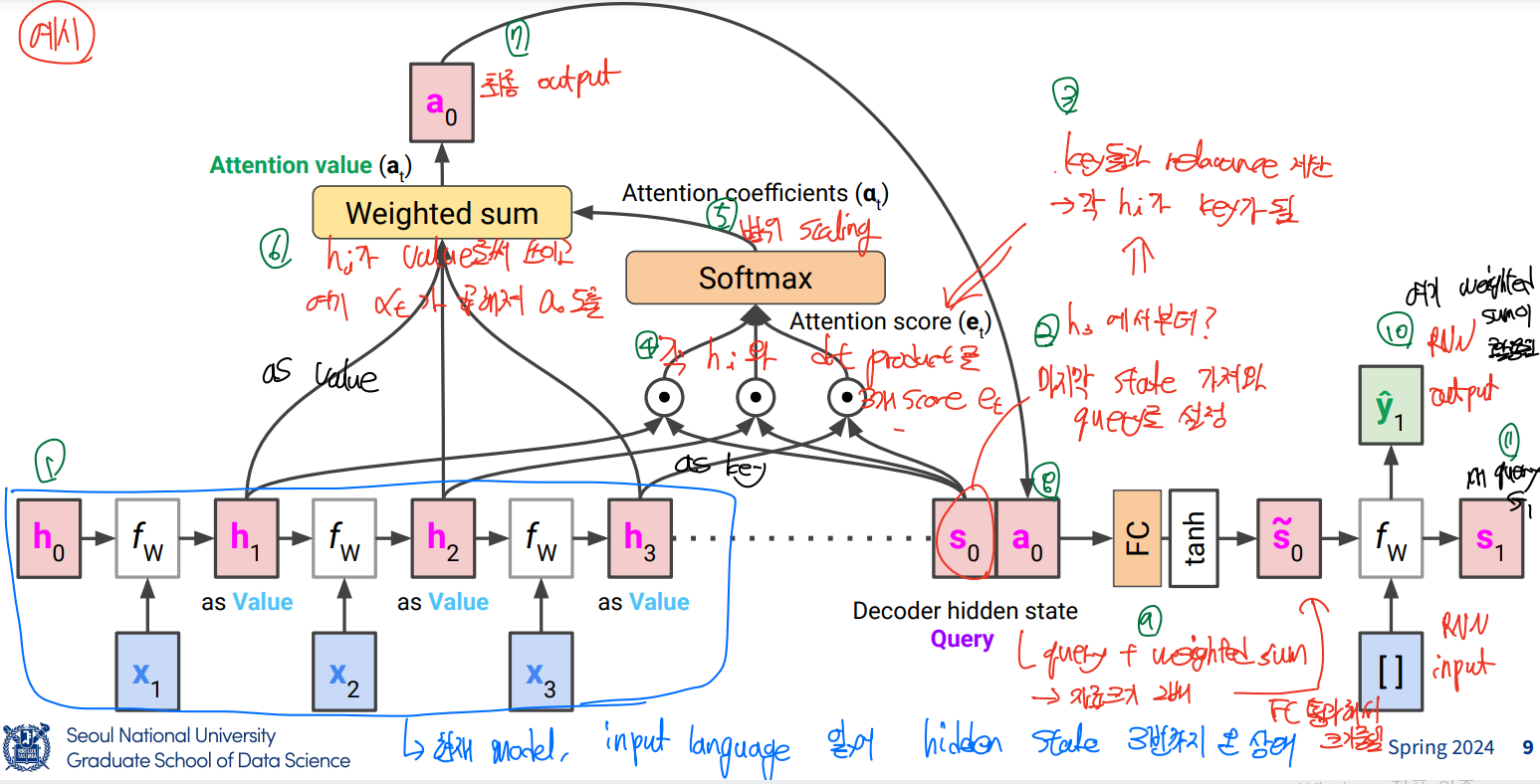
Q (Query): the decoder hidden state at time t , K (Keys): the encoder hidden states at all times , V (Values): the encoder hidden states at all times
-
encoder로 input, input 마지막 state 가져와서 query로 설정 → 각 hi가 key가 되어 key들과 relevance를 계산 (각 hi와 s0간 dot product로 각 attention score 계산 후 softmax를 거쳐 attention coeffieients 계산) → 이후 hi가 value로 쓰이고 여기 attention coefficient가 weight로 곱해져 a0를 최종 output으로 도출 → query와 weighted sum을 input으로 받아 s tilde를 출력하는 FC를 거치고, RNN input(첫 state이므로 sos)을 받아 RNN output을 출력 → 새 query인 s1로 넘어가 계속
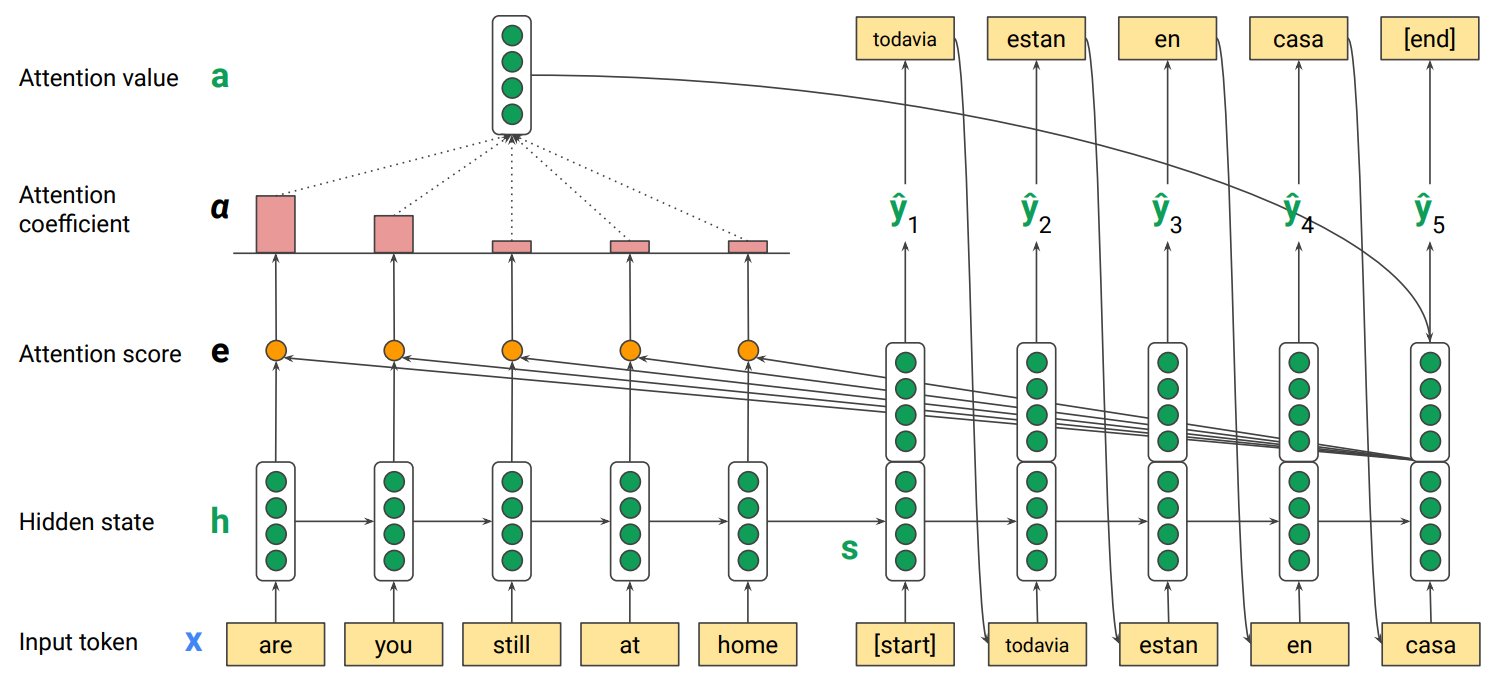
Transformers
input x가 서로 유기적으로 연결된 multiple element로 쪼개질 수 있다는 가정에서 시작함.
self attention → 각 element는 context(weighted sum of other elements)에 따라 자신의 representation을 수정함.
Transformer의 앞의 방식을 쓰려면 Q,K,V는 어떤걸 써야 하는가
값을 만들어서 사용함. input token (각 단어,들로 구성된 문장 )을 Q,K,V로 만들 때 linear transformation을 적용해서 Weight (Wq,Wk,Wv)를 곱하는 방식으로 QKV를 만듬 → 이 W를 학습함. 하나의 value를 가지고 weight만 다르게 하여 QKV를 각각 만들게 되는거, 모든 input에서 같은 W를 써야 한다.
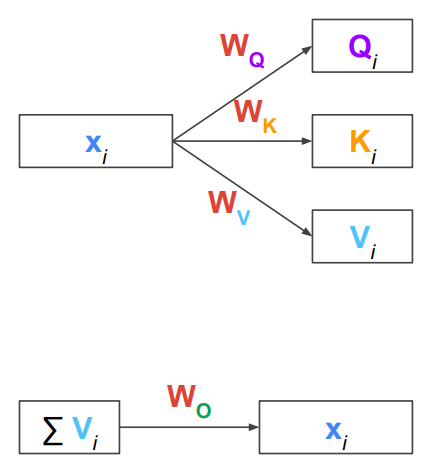
attention을 돌리고 output을 구하는게 value의 weighted sum임. 이 때 x가 아닌 V를 쓰므로? 다시 원래 크기로 돌려줘야하는데, 이 떄 Wo를 추가 도입
3개 token 예시에서, 1번째 token에서 attention을 할 때 Q K V 가 필요함. X1에 Wq를 곱해 Q1를 만듦. 이 Q와 Key와의 similartiy를 구해야함. 이 key는 각 x1,x2,x3에 해당되어야 하는데, 각 x에 대한 대리인 개념. Q1과 각 K간의 dot product로 coefficient 구하고, 각 value에 곱해서 더해야 하는데, 이 경우 각 x에서 Wv를 곱해 각 V를 만들어냄.
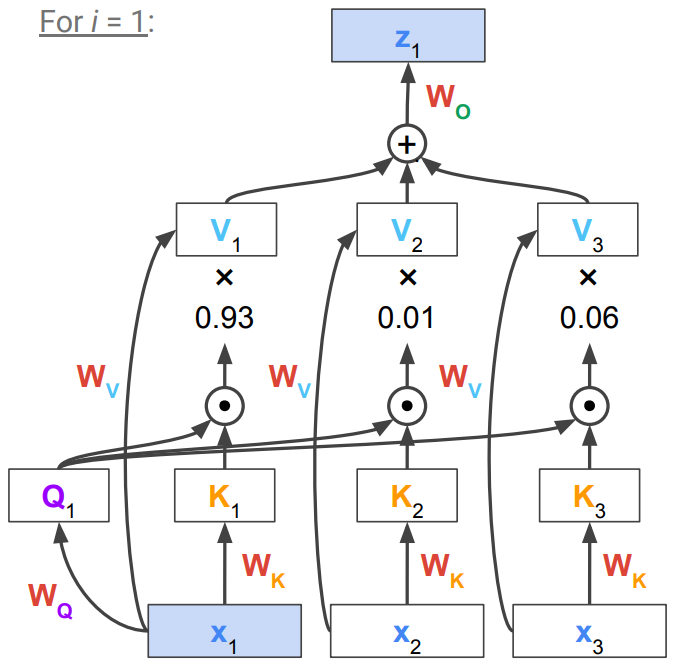
X1이 대부분이지만 context를 조금 포함한 새로운 z1으로 transformed
→이걸 각 x에 대해 반복해 각 z를 만들어냄.
이 과정을 여러 transformer 층을 쌓아서 만들 수도 있다.
앞에서 본 transformer의 문제
-
transformer의 input은 sequence여야 하고, 출력도 모두 sequence로 일대일 대응이 됨.
→ output의 형식이 고정됨. 이 sequence로 어떻게 써먹을건지 -
학습을 어떻게 시킬건지
-
RNN과 달리 token의 순서가 무시되는 것으로 보임
1번의 경우 가장 간단한 방법은 최종 sequence를 평균내기 →그러나 한계가 명확함
더 좋은 방법은 (여러개를 하나로) attention을 다시 써보는 것.
attention은 결국 input value의 weighted average였음. 여기서 어떻게 weight를 줄 것인가에 대한 논의를 했었음. 그러나 결국 하나의 단어에 문맥이 좀 더 추가된 것이기에 단어 하나만으론 classification이 불가능
→ dummy token(classification token, CLS)을 하나 추가함. → transformer 통과 후 문맥이 섞인 z0이 나옴. (토큰이 균등하게 나온 형태가 될 것) → 이 z값을 classifier에 넣고, classifier를 학습함.
위의 것이 sequence level의 prediction이고, token level이 필요하면 각 Zi를 classifier에 넣으면 됨
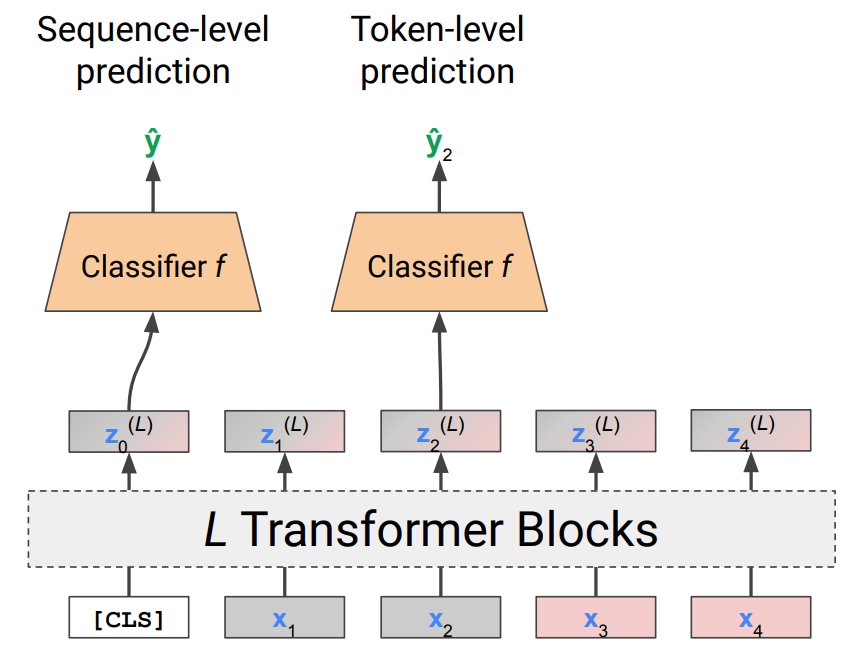
Inside the transformer
-
Input Embedding
- Input is a sequence of tokens.
-
Contextualizing the Embeddings
-
input embadding X를 가지고 Q, K, V를 각 Weight를 사용하여 만들어냄.
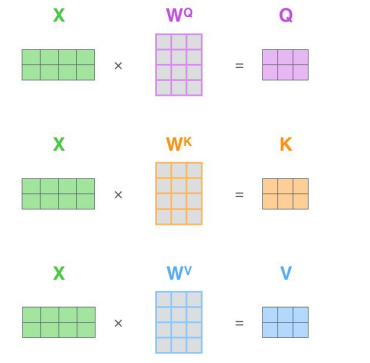
-
self attention이 적용됨.
-
각 input word에 대한 query에서, 자신을 포함한 모든 word의 key와의 similarity를 계산
-
자신을 포함한 모든 word의 value가 weighted된 sum인 attention value Z를 계산함.
-
Z= contexturalized new word embadding of same size

-
Multi-head self atention이 좋을 수도 있음.
- QKV를 여러 개 만들어서 여러개의 output(Z)이 나오면 이 output을 linear transform인 W0 weight를 곱해서 더함.
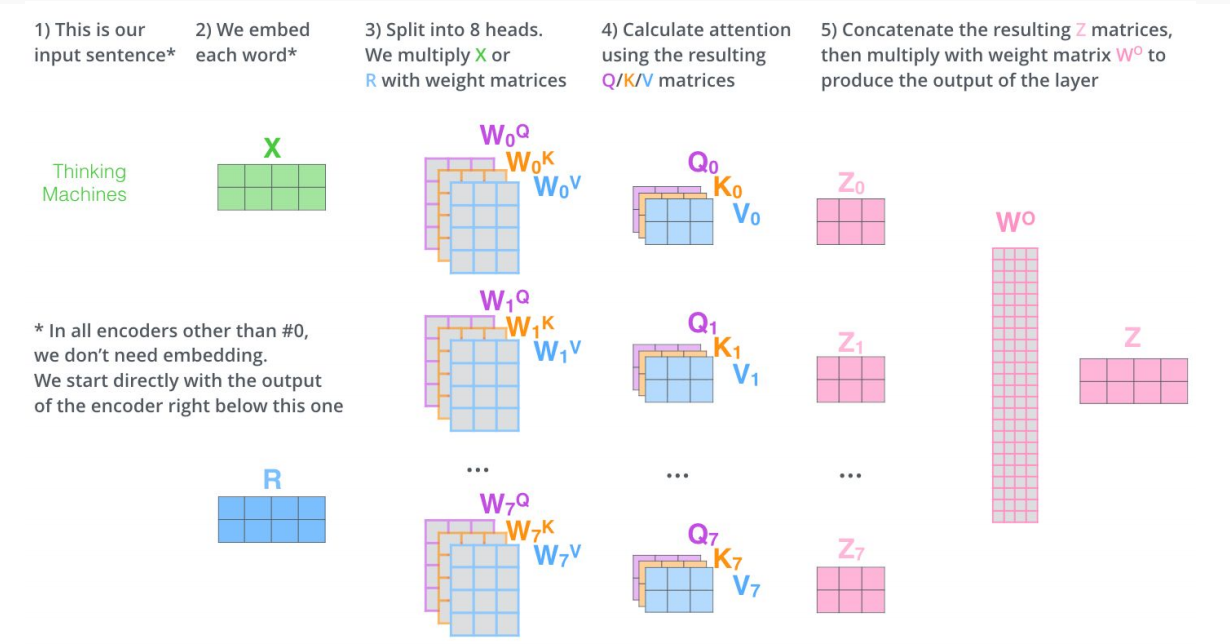
-
-
-
Feed-forward Layer
- 별도의 FC layer를 통과시킴. 다른 토큰과 상관없이 독자적으로 돌아가는 layer.
- Residual connection and layer normalization 거침.
- 이걸 N번 stack
- positional encoding이 input과 layer사이에 들어감.
- 여기선 RNN과 다르게 순서의 개념이 없기 때문에 거치는 과정
-
Decoder input
- Z를 받아서 output sequence를 auto-regressively 생성함
-
Masked Multi-head Self-attention
- 항상 토큰과 같은 사이즈의 시퀀스가 나오는 것을 방지하고자 더미 마스크 토큰을 추가함. → masking purpose
-
Encoder-Decoder Attention
-
Feed-forward Layer
-
Linear Layer
-
Softmax Layer
Bidirectional Encoder Representations from Transformers (BERT)
Large-scale pre-training of word embeddings using Transformer encoder
Transformer for Image Data
ViT (vision transformer)
다른건 거의 비슷하고, 이미지를 시퀀스화해서 적용함.
이미지의 16x16 patches는 하나의 token과 같다. 일정한 크기로 쪼개서 하나의 시퀀스로 사용.
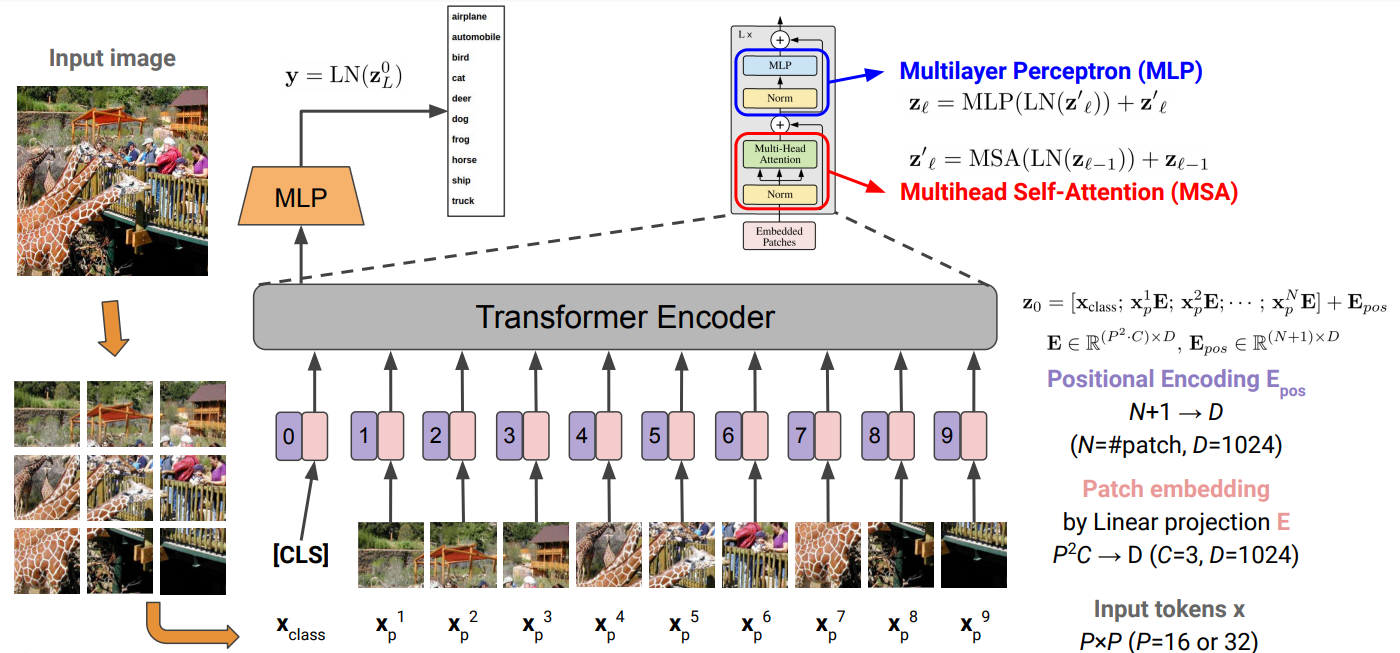
각 PxP 픽셀 쪼개진 패치에서, P^2C를 D로 linear projection
positional encoding은 이미지 상 위치임으로, 각 위치를 학습시켜버림.
이후는 앞과 동일함.